基于符号模拟的电路中错误诊断方法研究
时间:10-22
来源:EDN
点击:
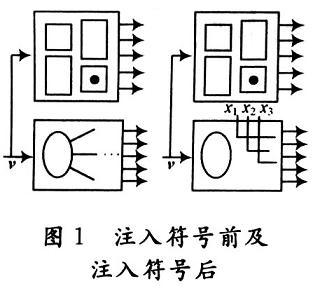 |
符号注入的作用是通过函数向主要输出方向传播来对区域A输出的扇出区域中的信号进行赋值。符号传播的过程类似于错误模拟过程,不同之处在于符号传播中一个信号的值不再是逻辑值0/1,而是用所注入的布尔变量{x1,x2,…,xk}表示的一个布尔函数。图2所示为符号传播过程。
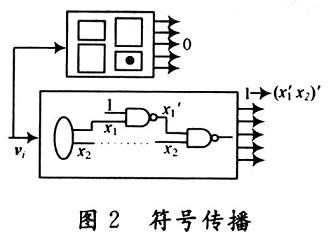 |
在符号传播过程中可以采取两项技术来加速该过程。一个是有序二叉决策图(OBDD)的使用,另一个是事件驱动的模拟。BDD的使用有可能造成内存爆炸,但是这里由于诊断过程中不需要特征化电路的全局函数,因此避免了上述内存爆炸问题。在事件驱动模拟中,许多门元件由于不受符号注入的影响,不需要进行再次模拟,因此在符号传播的一次单一运行中,CPU的处理时间不会因为电路规模的增大而迅速增加。
3.3 可治疗性检查
符号传播过程的最后可以在实现电路的每个主要输出得到一个布尔函数,称为作用函数。一个作用函数包含它对区域输出{a1,a2,…,ak}的一个注入起怎样反应的相关信息。通过对这些信息的获得可以计算区域中可治疗输入和可治疗输出的个数。
定义9 令Ii是第i个主要输出。v是一个错误输入向量,A是一个待检查的错误候选者区域。在向量v对实现电路进行模拟以及对区域A的输出进行符号注入和符号传播过程后,Ii的作用函数表示为Reacti(v,a,X),其中X是执行符号注入时所使用的布尔变量{x1,x2,…,xk}的集合。
命题1 当且仅当下面式子成立时,错误输入向量v是区域A的一个可治疗向量。Si(v)表示在向量v模拟下规范的第i个输出响应,n是输出的总个数。
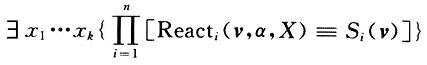 |
证明 如果存在{x1,x2,…,xk}的一个注入组合,使得注入后对于每一个主要输出索引i,实现电路的Reacti(v,a,X)的响应同规范Si(v)的响应值相同,则该注入组合被称为区域可治疗注入,同时也证明了在区域A的输出处注入的组合使得错误输入向量v不再引起任何输出对之间的不匹配现象,即v不再是实现电路的一个错误输入向量。
如果存在一个注入组合,使得一个不匹配输出的逻辑值变为与它对应的完全相同的值,则称该不匹配输出为一个区域可治疗输出(区域可治疗输出的规则):如果下面的条件成立,则对于向量v,一个不匹配输出Zic称为通过区域输出信号a的可治疗输出。
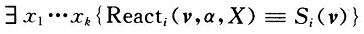 |
例如(区域可治疗注入)考虑图中的规范和实现,在一个输入向量v的模拟下,规范的输出响应为(0,O,0,0,0),而实现的响应为(0,0,0,1,1)。第四和第五个输出为不匹配输出。通过执行符号注入和传播,每个主要输出作用函数的集合为{0,0,x3,x1,(x1x2)'}。
前两个输出对是匹配的,因此只进行后三个输出的可治疗性检查。为了检查可治疗向量,注入需满足(x3三0),(x1三O)和[(x1x2)'三0]。因为第二个和第三个条件互相冲突,可得出结论:区域A不能通过注入来治疗错误输入向量v。
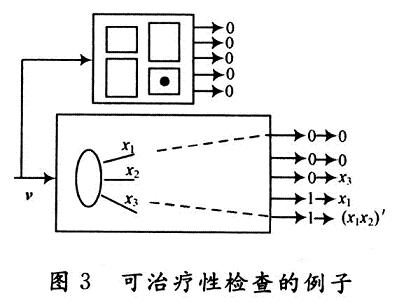 |
另一方面,为可治疗输出检查每个作用函数。在注入前只需要关注于第4和第5个不匹配输出。第4个输出的作用函数是x1,只需要在注入时使x1为0,就可使输出从1变为0,即通过此方法解决了第4个输出的不匹配问题,因此第4个输出是一个可治疗输出。类似地,第5个输出也是可治疗输出。因此该区域A共有两个可治疗输出。在这个例子中,两个不匹配输出可以分别独立地进行治疗纠正;然而在治疗最后一个输出时将不可避免地在第3个输出点引出一个新的不匹配问题,这也是给定的错误输入向量不能通过区域A来治疗纠正的原因。利用符号模拟技术可以优化基于区域模型进行错误诊断的过程,依据区域可治疗向量和区域可治疗输出两个测量标准对候选的各个区域进行包含错误点的可疑度等级排序,可疑度等级越高的区域,包含错误点的可能性也越大。
