1 引言 整流电路(Rectifier)尤其是单相桥式可控整流电路是电力电子技术中最为重要,也是应用得最为广泛的电路,不仅应用于一般工业,也广泛应用于交通运输、电力系统、通信系统、能源系统等其他领域。因此对单相桥式可控整流电路的相关参数和不同性质负载的工作情况进行对比分析与研究具有很强的现实意义,不仅是电力电子电路理论学习的重要一环,而且对工程实践的实际应用具有预测和指导作用。
2 单相桥式半控整流电路 图1中VT1和VT2为触发脉冲相位互差180?的晶闸管,VD1和VD2为整流二极管,由这四个器件组成单相桥式半控整流电路。电阻R和电感L为负载,若假定电感L足够大,即ωL≥R,由于电感中电流不能突变,可以认为负载电流在整个稳态工作过程中保持恒值。由于桥式结构的特点,只要晶闸管导通,负载总是加上正向电压,而负载电流总是单方向流动,因此桥式半控整流电路只能工作在第一象限,因为ωL≥R,所以不论控制角α为何值,负载电流id的变化很小。
| 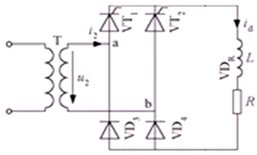
图1 单相桥式半控整流电路原理
在u2正半周,触发角α处给晶闸管VT1施加触发脉冲,u2经VT1和VD4向负载供电。u2过零变负时,因电感作用电流不再流经变压器二次绕组,而是由VT1和VD2续流。此阶段若忽略器件的通态压降则负载压降ud不会出现负的情况。在u2负半周触发角α时刻,VT2与VD3触发导通,同时向VT1施加反向电压并使之关断,u2经VT2和VD3向负载供电。u2过零变正时,VD4导通,VD3关断。VT1和VD4续流,负载压降ud又变为零。
根据上述分析,可求出输出负载电压平均值为:
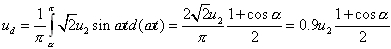 (1) (1)
α角的移相范围为180°。输出电流的平均值为:
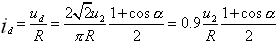 (2) (2)
流过晶闸管的电流平均值只有输出直流平均值的一半,即:
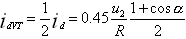 (3) (3)
流过晶闸管的电流有效值:
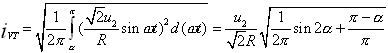 (4) (4)
单相桥式半控整流电路的仿真模型如图2所示。
| 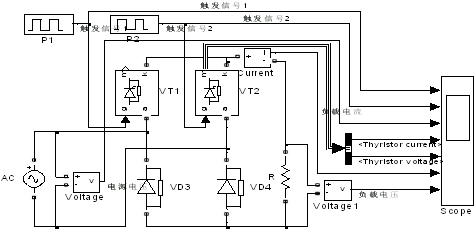 图2 单相桥式半控整流电路的仿真模型 (1)带纯电阻性负载情况
相应的参数设置:① 交流电压源参数U=100V,f=50Hz;② 晶闸管参数Rn=0.001Ω,Lon=0H,Vf=0.8V,Rs=10Ω,Cs=250e-6F;③ 负载参数R=10Ω,L=0H,C=inf;④ 脉冲发生器触发信号1、2的振幅为5V,周期为0.02s(即频率为50Hz),脉冲宽度为2。
设置触发信号1的初相位为0s(即0?),触发信号2的初相位为0.01s(即180?),此时的仿真结果如图3(a)所示;设置触发信号1的初相位为0.0025s(即45?),触发信号2的初相位为0.0125s(即225?),此时的仿真结果如图3(b)所示。 | 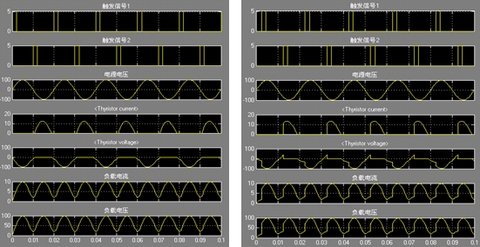 (a) (b)
图3 带纯电阻性负载单相桥式半控整流电路的仿真模型:
(a)控制角为0?;(b)控制角为45?
(2)带电阻电感性负载情况
带电阻电感负载的仿真与带纯电阻负载的仿真方法基本相同,只需将RLC串联分支负载参数设置为R=1Ω,L=0.01H,C=inf。此时的仿真结果分别如图4(a)、图4(b)所示。 | 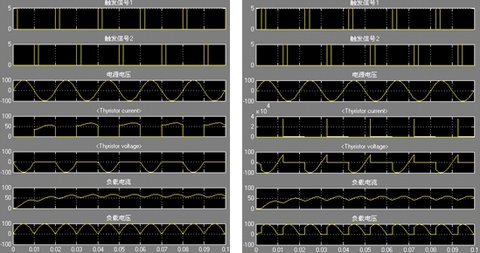
(a)(b)
图4 带电阻电感性负载单相桥式半控整流电路的仿真模型:
(a)控制角为0? ;(b)控制角为45? 3 单相桥式全控整流电路
单相可控整流电路中应用最多的是单相桥式全控整流电路(Single Phase Bridge Full-Controlled Rectifier),如图5所示。在单相桥式全控整流电路中,每一个导电回路中有2个晶闸管,即用2个晶闸管同时导通以控制导电的回路。 | 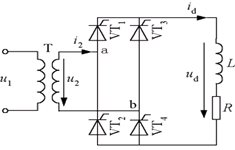 图5 单相桥式全控整流电路原理 上文已经就单相桥式半控整流电路在纯电阻性负载时进行了较为详尽的分析,而且全控电路与半控电路在纯电阻性负载时的工作情况基本一致,同时晶闸管承受的最大正向电压和反向电压也同前述电路相同,分别为和。
以下重点分析带电阻电感负载时的工作情况。
VT1和VT4组成一对桥臂,在u2正半周(即a点电位高于b点电位)承受电压u2,若在触发角α处给晶闸管VT1和VT4施加触发脉冲使其开通,电流从电源a端经VT1、R、VT4流回电源b端,ud=u2。在u2过零时关断。假设电路已工作于稳态,id的平均值不变。负载中有电感时电流不能突变,电感对负载电流起平波作用,假设负载电感很大,负载电流id连续且近似为一水平直线,u2过零变负时,由于电感的作用晶闸管VT1和VT4中仍流过电流id,并不关断。
VT2和VT3组成另一对桥臂,在u2正半周承受电压-u2,至ωt=π+α时刻,给VT2 和VT3施加触发脉冲,因为VT2 和VT3本已经承受正向电压,故两管导通。在u2过零时关断。VT2 和VT3导通后,分别给VT4 和VT1施加反向电压使其关断。流过VT1和VD4的电流迅速转移到VT2 和VT3上,此过程称为换相,亦称换流。在下一周期重复相同过程,如此循环。
若4个晶闸管均不导通,则负载电流id为零,负载电压ud也为零。
根据上述分析,可求出输出负载电压平均值为: | | | | |


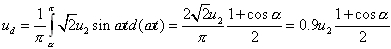 (1)
(1) 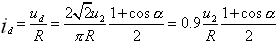 (2)
(2) 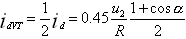 (3)
(3) 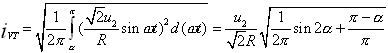 (4)
(4) 


