无独立源单口电路的输入电阻及其等效电路

　　对于无独立源单口电路具有两个引出端钮,内部无独立电源且两个端钮上的电流为同一电流的部分电路称为无独立源单口电路,也称为无独立源一端口电路, ，如图2-4-1(a)所示，我们引入输入电阻(也称等效电阻)的概念,用R0表示.其定义为端口电压u与端口电流i之比,即 R0=u/i

　　输入电阻R0的倒数称为无独立源单口电路的输入电导,用G0表示.即 G0=1/R0=i/u

　　根据上两式即可作出与之对应的等效电路,如图2-4-1(b)所示.此电路称为无独立源单口电路的等效电路.但要注意,这里的"等效"仍是指对无独立源单口电路以外的电路等效,即当用等效电阻R0代替了原无独立源单口电路后,端口上的电压u与电流i的关系曲线不便.

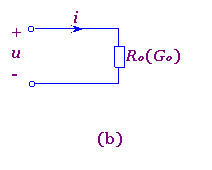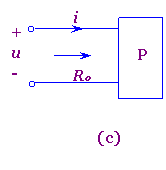　　　　　　　　　　　　　　　　　　图2-4-1 无独立源单口电路及其等效电路
　　以下分两种电路来研究输入电阻R0的求解方法.
一. 无任何电源的单口电路
　　不含任何电源(独立源与受控源)的单口电路,通常用方框内写以字母P表示,如图2-4-1(c)所示.其输入电阻R0可通过星形-三角形等效变换,电阻串联与并联化简的方法求得.
例2-4-1 图2-4-2(a)电路.求等效电阻Rab与各支路电流？

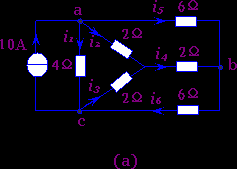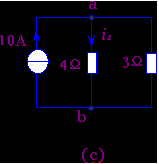图2-4-2 例2-4-1的电路

　　解: 将星形联接的三个2Ω电阻等效变换为三角形联接的三个6Ω联接电阻,如图2-4-2(b)所示.然后再利用电阻串并联简化原则,将图(b)电阻简化成图(c)所示电阻.于是根据图(c)
得 Rab=4×3/4+3=12/7 Ω
i1=30/7 Ω
uab=4i1=120/7 V
再回到图(b)电路得 i2=uab/6=20/7 A
i3=i4=i5=i6=(10-i1-i2)/2=10/7 A
再回到图(a)电路得 i2=10-i1-i5=30/7 A
i3=i1+i6-10=-30/7 A
i4=i6-i5=0

二. 含受控源的单口电路
　　含受控源的单口电阻可通过等效变换求得其等效电阻.在进行等效变换时,受控源与独立源同样处理,但必须把控制变量所在的支路保留不动,然后在根据所得到的简化电路,应用在网络端口处外施电压源u以求端口电流i,或外施电流源i以求端口电压u的方法,按式R0=u/i来求其等效电阻.
例2-4-2 求图2=4=3(a)所示单口网络的输入电阻(等效电阻)R0?

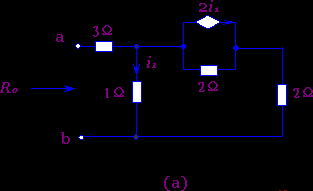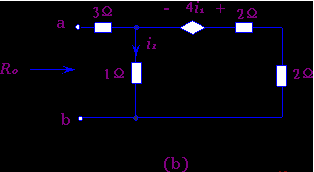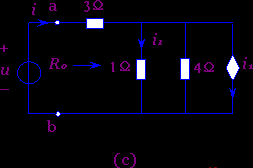图2-4-3 含受控源的单口电路

　　解: 首先将受控电流源2i1与2Ω电阻的并联组合,等效变换为受控电压源4i1与电阻2Ω的串联组合,其变换原则与独立电压源和独立电流源的相互等效变换原则全同,如图2-4-3(b)所示.然后再将受控电压源4i1 与电阻(2Ω+2Ω)的串联组合,等效变换为受控电流源i1与电阻4Ω的并联组合,如图2-4-3(c)所示.可见简化后的电路图(c),保留了控制变量 i1支路不动.于是根据图(c)电路,从端口ab处外施以电压u以求得电流i即:
;i=i1+(u-3i)/4+i1

又有 i1=(u-3i)/1

联解得输入电阻(等效电阻)为:R0=u/i=31/9 Ω
其等效电路如图2-4-3(d)所示.可见含线性受控源的单口网络的等效为一线性电阻元件,从而表明了受控源的电阻性.