反激电源以及变压器设计

         对于探讨反激电源以及变压器这个话题，我犹豫了很久。因为关于反激的话题大家讨论了很多很多，这个话题已经被讨论的非常透彻了。关于反激电源的参数设计也有多篇文章总结。还有热心的网友，根据计算过程，自己编写了软件或电子表格把计算做的傻瓜化。但我也注意到，几乎每天都会出现关于反激设计过程出现问题而求助的帖子，所以，思量再三，我决定还是再一次提出这个话题!我不知道我是否能写出一些有新意的东西，但我会尽力去写好。不期望能入高手的法眼，但愿能给入门者一些帮助。

　　纵观电源市场，没有哪一个拓扑能像反激电路那么普及，可见反激电源在电源设计中具有不可替代的地位。说句不算夸张的话，把反激电源设计彻底搞透了，哪怕其他的拓扑一点不懂，在职场上找个月薪10K的工作也不是什么难事。

　　提纲

　　1、反激电路是由buck-boost拓扑演变而来，先分析一下buck-boost电路的工作过程。

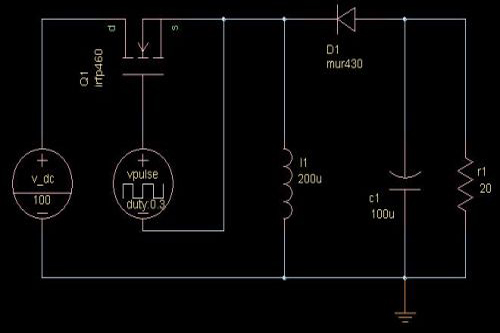
　　工作时序说明：

　　t0时刻，Q1开通，那么D1承受反向电压截止，电感电流在输入电压作用下线性上升。

　　t1时刻，Q1关断，由于电感电流不能突变，所以，电感电流通过D1，向C1充电。并在C1两端电压作用下，电流下降。

　　t2时刻，Q1开通，开始一个新的周期。

　　从上面的波形图中，我们可以看到，在整个工作周期中，电感L1的电流都没有到零。所以，这个工作模式是电流连续的CCM模式，又叫做能量不完全转移模式。因为电感中的储能没有完全释放。

　　从工作过程我们也可以知道，这个拓扑能量传递的方式是，在MOS管开通时，向电感中储存能量，MOS管关断时，电感向输出电容释放能量。MOS管不直接向负载传递能量。整个能量传递过程是先储存再释放的过程。整个电路的输出能力，取决于电感的储存能力。我们还要注意到，根据电流流动的方向，可以判断出，在输入输出共地的情况下，输出的电压是负电压。

　　MOS管开通时，电感L1承受的是输入电压，MOS关断时，电感L1承受的是输出电压。那么，在稳态时，电路要保证电感不进入饱和，必定要保证电感承受的正向和反向的伏秒积的平衡。那么：

　　Vin×(t1-t0)=Vout×(t2-t1)，假如整个工作周期为T，占空比为D，那么就是：Vin×D=Vout×(1-D)

　　那么输出电压和占空比的关系就是：Vout=Vin×D/(1-D)

　　同时，我们注意看MOS管和二极管D1的电压应力，都是Vin+Vout

　　另外，因为是CCM模式，所以从电流波形上可以看出来，二极管存在反向恢复问题。MOS开通时有电流尖峰。

　　上面的工作模式是电流连续的CCM模式。在原图的基础上，把电感量降低为80uH，其他参数不变，仿真看稳态的波形如下：

t0时刻，Q1开通，那么D1承受反向电压截止，电感电流在输入电压作用下从0开始线性上升。