改善 RMS 功率检波器在整个温度范围内的输出准确度

引言   
在基站设计中，稳定的温度性能极其重要，因为视基站周边情况和地点的不同而不同，环境温度可能变化很大。RMS 检波器如果随温度变化的准确度很高，就可以提高基站设计的电源效率。LTC5582 和双通道 LTC5583 是一个 RMS 检波器系列的两款器件，LTC5582 在最高 10GHz 的频率范围内可提供极其稳定的温度性能 (从 -40°C 至 85°C)，而 LTC5583 的频率范围则在 6GHz 内。不过，它们的温度系数随频率而改变，而没有温度补偿下，随温度变化而产生的误差可能大于 0.5dB。因此，有时有必要针对不同的频率优化温度补偿，以改善准确度，使误差 <0.5dB。此外，温度补偿可以仅用两个外部电阻器实现，而无需外部电路。
输出电压的变化由以下等式决定：
?VOUT = TC1 x (TA - tNOM) + TC2 x (TA - tNOM)2 + detV1 + detV2         (等式 1)
其中 TC1 和 TC2 分别是 1 阶和 2 阶温度系数。TA 是实际的环境温度，tNOM 是室内基准温度25°C，detV1 和 detV2 是 RT1 和 RT2 未设定为零时的输出电压变化。

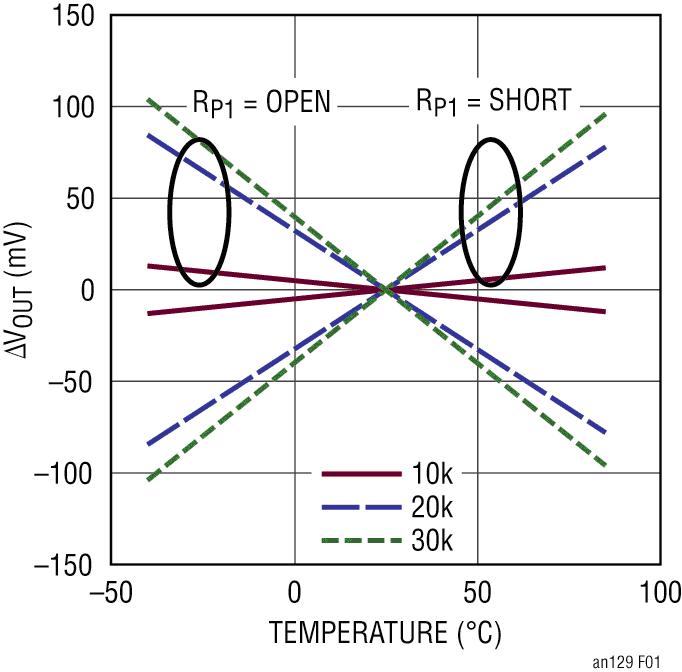
图 1：1 阶 ?VOUT 随温度的变化

就 LTC5582 和 LTC5583 而言，计算温度补偿电阻值的方法是相同的 (参见图 2 和图 3)。两个控制引脚是 RT1 和 RT2，RT1 设定 TC1 (1 阶温度补偿系数)，RT2 设定 TC2 (2 阶温度补偿系数)。如果不需要温度补偿，那么将 RT1 和 RT2 短路到地，就可以很方便地关闭温度补偿功能。

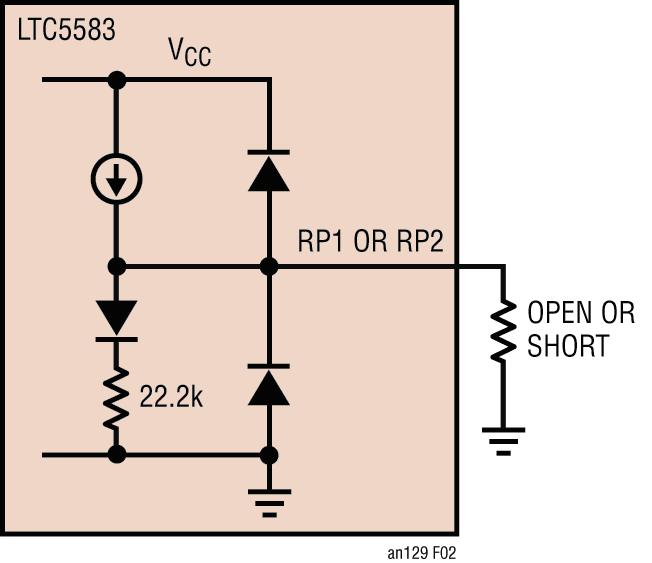
图 2：引脚 RP1 和 RP2 的简化原理图

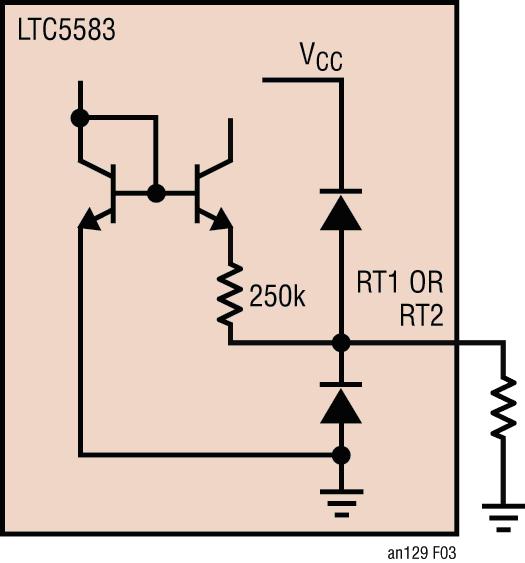
图 3：引脚 RT1 和 RT2 的简化原理图

LTC5583 的温度补偿设计
LTC5583 包括两个额外的引脚 RP1 和 RP2，RP1 控制 TC1 的极性，RP2 控制 TC2 的极性。不过，在采用一个固定的 RT1 或 RT2 值时, 温度系数的大小相等, 只是极性倒转。通道 A 和通道 B 共享补偿电路，因此两个通道一起受到控制。
图 1 说明了在 1 阶温度补偿的情况下，VOUT 作为温度的函数是怎样变化的。图中仅显示了 3 个电阻值，以说明增大电阻值会使斜线斜率增大。斜线极性由 RP1 引脚控制。

图 4 说明了 2 阶温度补偿对 VOUT 的影响。该曲线的极性由 RP2 控制。其曲率取决于电阻值。1 阶和 2 阶温度补偿合起来的总体影响由等式 1 给出。

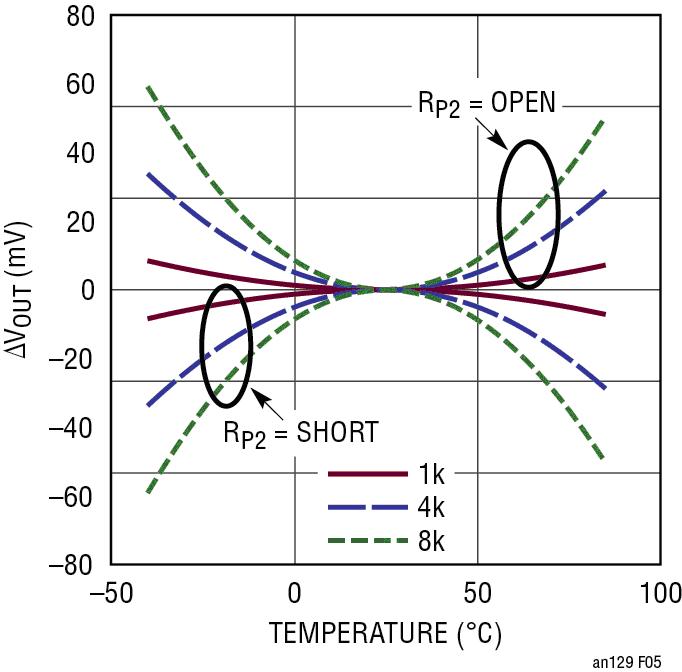
图 4：2 阶 VOUT 随温度的变化

以 LTC5583 在 900MHz 输入时的情况为例。第一步是测量没有温度补偿时 VOUT 随温度的变化。图 5 显示未补偿时的 VOUT。线性误差随温度的变化以 25°C 时的斜线和截取点为基准。为了最大限度地减小输出电压随温度的变化，红色 (85°C) 的线性度曲线必须下移，蓝色 (-40°C) 的线性度曲线必须上移，以与黑色室温时的曲线一致，并尽可能多地重叠。接下来就是一步一步地设计了。

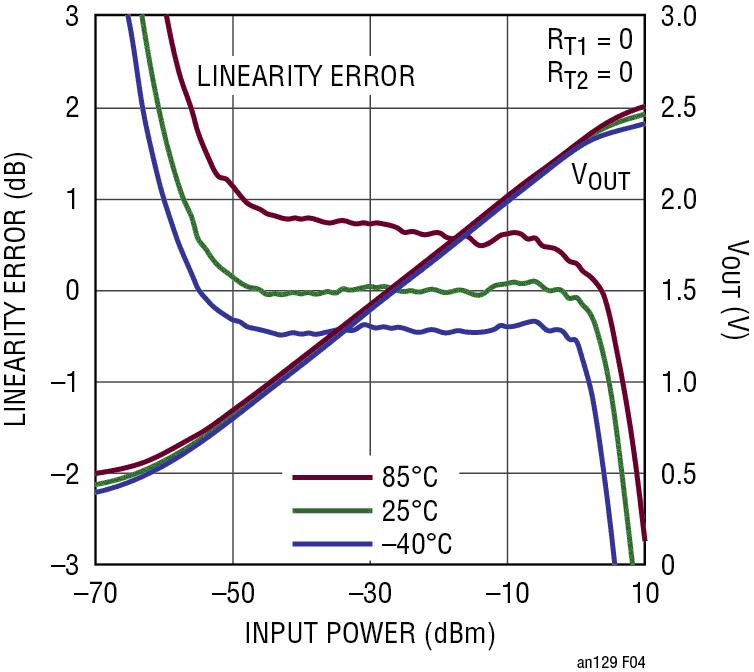
图 5：在 900MHz 时未补偿的 LTC5583

第一步。以 dB 为单位从图 5 估计所需的温度补偿。例如，读取输入功率为 -25dBm 时的曲线值，这是动态范围的中部。将以 dB 为单位的线性误差乘以 30mV/dB (典型的 VOUT 斜率)，以将单位转换为 mV。
低温 (-40°C) = +13mV 或 +0.43dB
 高温 (85°C) = -20mV 或 -0.6dB
这是随温度变化所需的输出电压调节量。
第二步。确定 RP1 和 RP2 的极性以及 1 阶和 2 阶补偿解决方案。为了找到解决方案，设 a = 1 阶项，b = 2 阶项。设定这两项的值，使它们满足  -40°C 和 85°C 的温度补偿要求。
a – b = +13mV     (等式 2)
a – b = -20mV     (等式 3)
a = 16.5   (1 阶解决方案)
b = 3.5（2 阶解决方案）
等式 2 和等式 3 中"a"和"b"的极性由 1 阶项和 2 阶项的极性决定，这样，它们的和在低温 (-40°C) 时满足 +13Mv 和高温时满足 -20mV (85°C) 的调节要求。参见图 6。1 阶项和 2 阶项或者为正、或者为负。因此。总共有 4 种组合。在这种情况下，仅当两项均为负时，它们的和才能满足所需补偿。

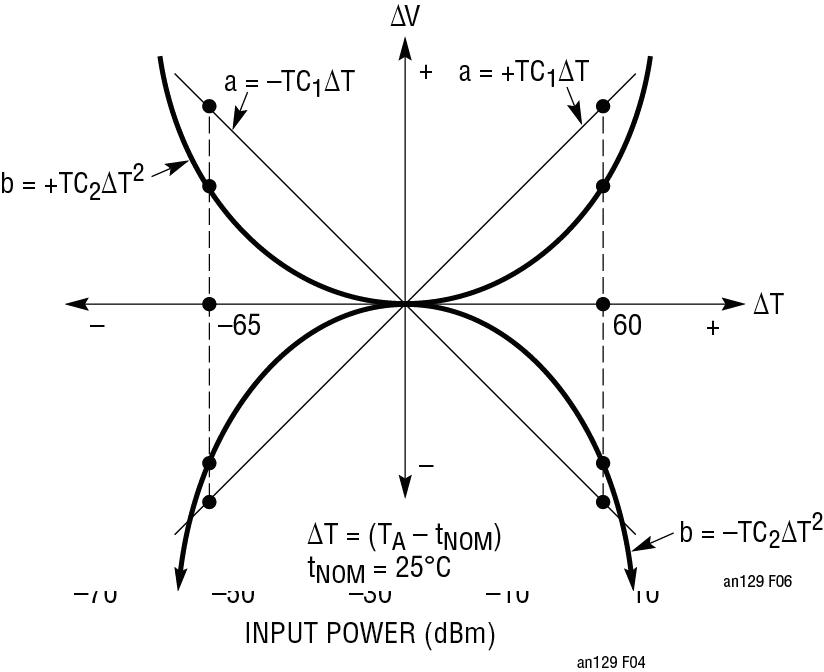
图 6：1 阶和 2 阶解决方案的极性


图 7 显示了在 -40°C 和 +85°C 时所需的 1 阶和 2 阶补偿。请注意，1 阶和 2 阶补偿的极性是负的，这样，当两条曲线相加时，它们的和才能对 VOUT 产生所需的调节。结果，TC1 和 TC2 为负，RP1 和 RP2 从图 8 和图 9 决定。请注意，两个解决方案的值加起来在 -40°C 时约等于 +13mV，在 +85°C 时约等于 -20mV。

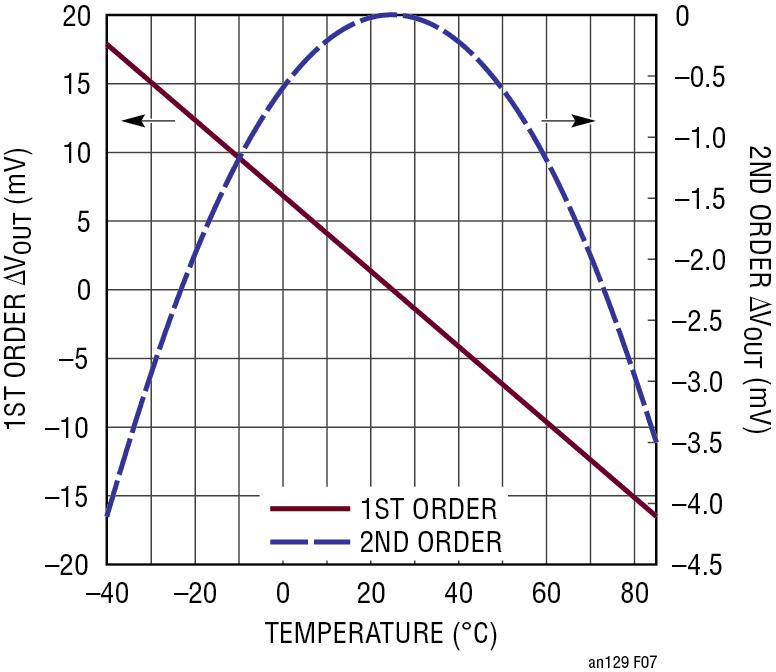
图 7：温度补偿解决方案

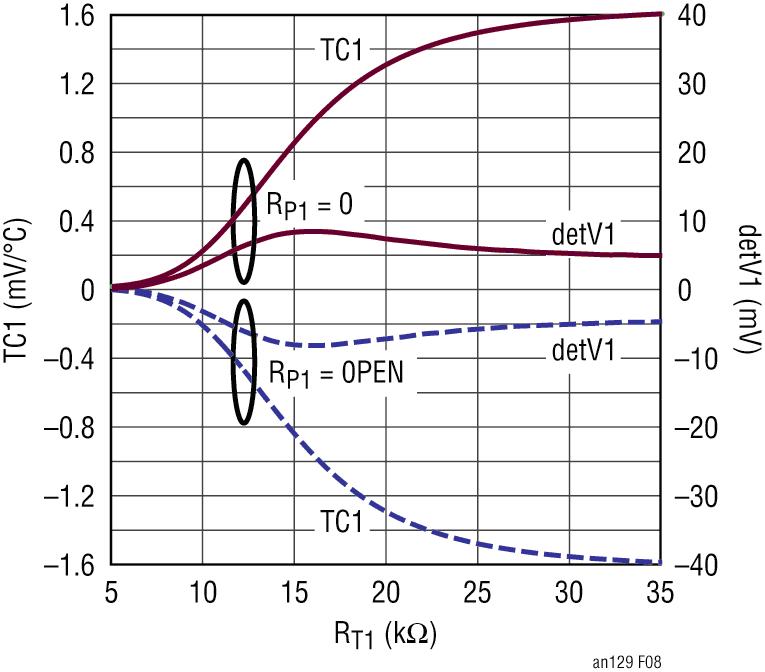
图 8：1 阶温度补偿系数 TC1 随外部 RT1 值的变化
 
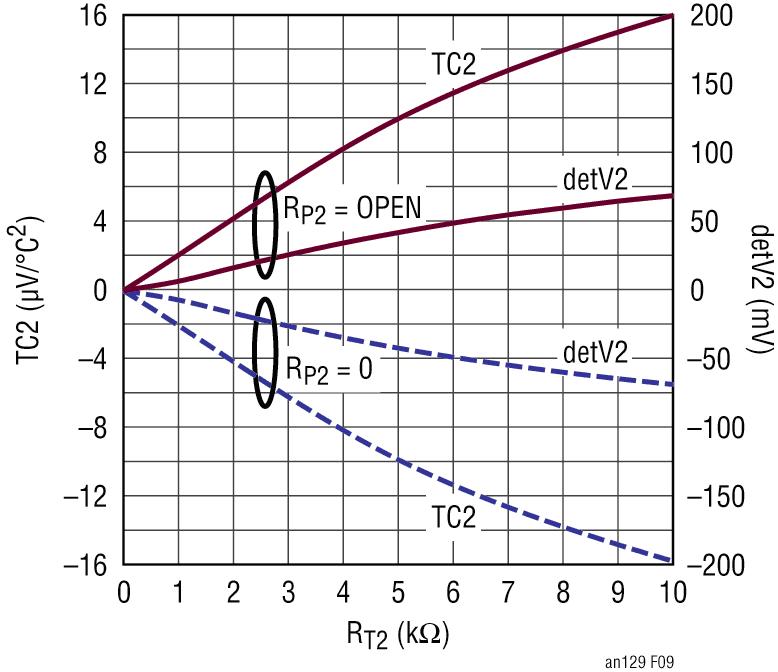
图 9：2 阶温度补偿系数 TC2 随外部 RT2 值的变化

RP1 = 开路
RP2 = 短路
第三步。计算一个温度极限的温度系数，利用图 8 和图 9 确定 RT1 和 RT2 的电阻值。
a = 16.5 =TC1 x (85 - 25)；TC1 = 0.275mV/°C
RT1 = 11K? (根据图 8)
b = 3.5 = TC2 x (85 - 25)2；TC2 = 0.972uV/°C2
RT2 = 499? (根据图 9)

图 10 显示了 LTC5583 的两个输出通道之一随温度变化的性能。请注意与图 5 中未补偿 VOUT 相比的温度性能改进。就大多数应用而言，这也许能满足要求了。不过，对于某些需要更佳准确度的应用, 可以执行二次迭代以进一步改善温度性能。为了简化计算可忽略 detV1 和 detV2 项，因为这两项不受温度影响。因此，解决方案是不精确的。不过，在改进随温度变化的准确度方面，这么做很有用，如下所示。

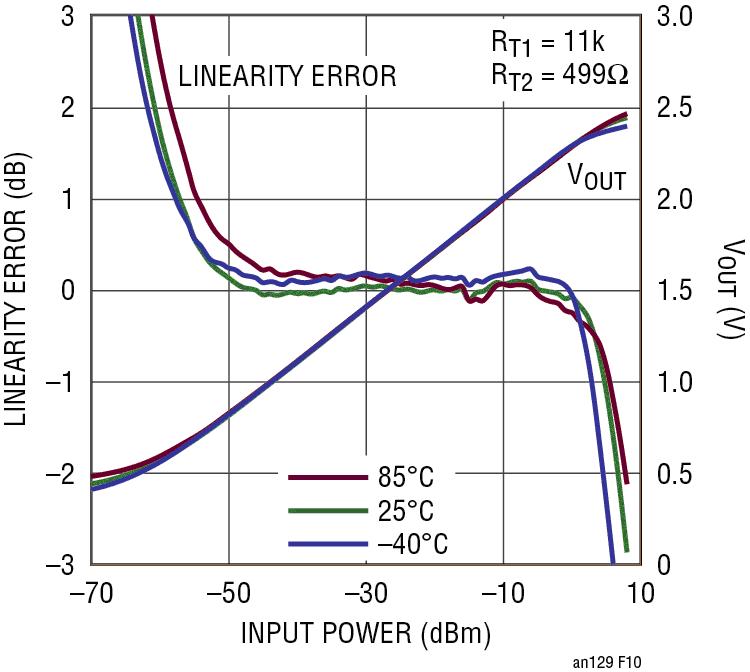
图 10：1 阶迭代温度补偿的 LTC5583 输出
2 次迭代计算
第一步。从图 10 中确定所需补偿，采用与第一次迭代时相同的方法。
低温 (-40°C) = -3mV 或 -0.1dB
高温 (85°C) = -3mV 或 -0.1dB
给 1 次迭代增加新值
低温 (-40°C) = -3mV + 13mV = 10mV
高温 (85°C) = -3mV - 20mV = -23mV
重复第二步和第三步，计算 RT1 和 RT2 值。
RT1 = 11K?
RT2 = 953?
RP1 = 开路
RP2 = 短路
经过两次迭代后的性能结果如图 11 所示。随着温度变化，动态范围为 50dB (0.2dB 线性误差) 和 56dB (1.0dB 的线性误差)。从表 1 中可查到其他频率时的温度补偿值。

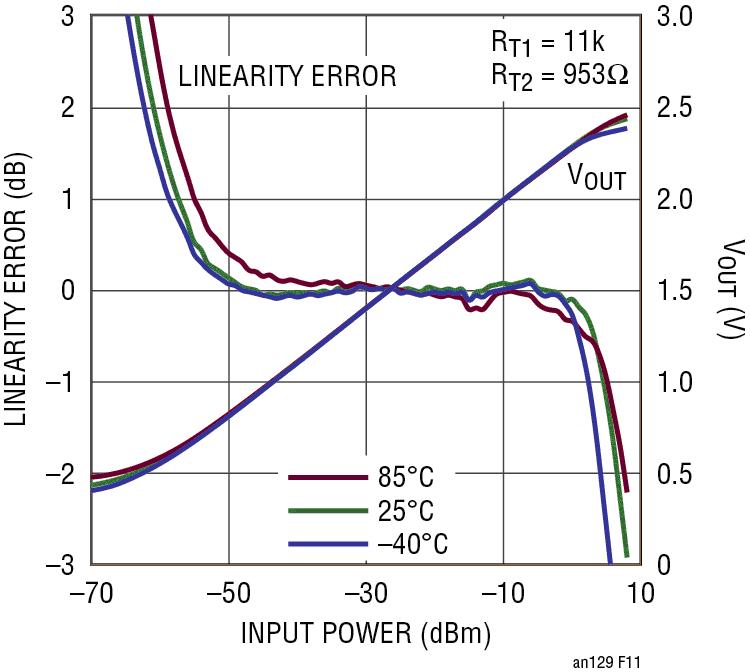
图 11：2 阶迭代后温度补偿的 VOUT

表 1：LTC5583 要在各种不同的频率时实现最佳的温度性能，推荐采用以下设定和电阻值