基于支持向量机的联机手写识别

F(X，Z)=exp(-y·DTW(X，Z)) (8)

他们的联机手写识别实验的结果和Bothe等人的实验结果表明，GDTW-SVM取得了比GDTW-SVM和k近邻算法(k-Nearest Neighbor，kNN)更高的识别率，而且在不同联机手写识别数据库子集的识别实验中，与基于其它弹性距离计算的核函数的SVM相比，各有优劣且识别率的差值在0．3％以内。

到字母n的所有训练样本最优对齐路径，并规整到80’80矩阵；

(2)将所有计算结果叠加后得到n-n最优对齐路径叠加图；

(3)绘制叠加图，即图2的第一幅图，图中像素点灰度越高，代表越多最优对齐路径经过此点。同理，绘制n-m最优对齐路径叠加图和m-m最优对齐路径叠加图，分别为图2的第二和第三幅图所示。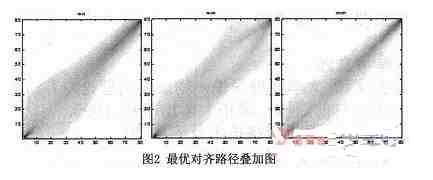

从图2可以看到，两个相同或相似字符的最优对齐路径集中在对角区域：由于n的不同样本、m的不同样本的起笔写法比收笔写法随意，第一和第三幅图的对角区域的左下角比较宽；n和m的最优对齐路径在对角区域中分布较均匀，且第二幅图显示对角区域的中部有明显的低灰度区域。

假设训练样本可以代表联机手写字符的特征，则可以通过仅计算对角区域中的最优对齐路径来优化GDTW核函数。计算两个样本T=(t1，…，tNT)和R=(r1，…，rNR)的GDTW核函数时，假定二者属于相同的字符类，那么二者的差别不大，因此，在GDTW核函数计算中引入参数k和τ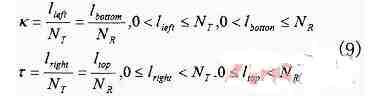

式(9)中lbottom，ltop，lleft，lright如图3所示。引入参数k和τ之后，不在NT×NR的矩阵中求解式(8)，而是在k和τ约束的区域(即图3中两条虚线所夹的对角区域)中求解，计算最优对齐路径。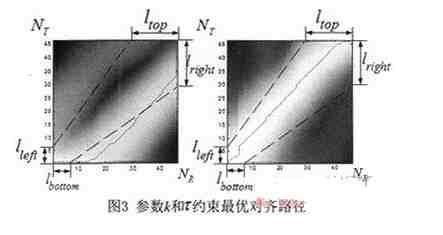

从直观的角度看，参数k和τ减少了最优对齐路径的计算空间，因此，修改后的GDTW核函数的计算时间减少。而另外一方面，如果参数τ保持不变(如τ=0．6)，参数k越小，最优对齐路径的前端的计算被约束在越小的空间，迫使其"最优"对齐路径的计算选择非最优对齐路径，即参数k是两个字符样本头部的相识程度的权重；类似地，参数τ是两个字符样本尾部的相识程度的权重。参数k和τ的权重作用对于如数字"0"和"6"等相似字符的分类有重要意义。

4 实验结果与分析

本文主要针对阿拉伯数字样本集和英文字母样本集进行识别实验，阿拉伯数字样本集、英文小写字母样本集和英文大写字母样本集分开识别。实验环境是Matlab R2010a，所使用的SVM工具包是Matlab SVM Toolbox。

分类实验采用Leave-One-Out的交叉验证策略：依次从样本集中取出一个字符的训练样本标记为第一类，将剩余字符的训练样本标记为第二类，用标记后的训练样本训练GDTW-SVM；使用样本集中的所有测试样本测试GDTW-SVM的识别率。

使用未优化GDTW-SVM重复分类识别10次，取10次实验结果的平均值作为未优化GDTW-SVM的识别结果；其次，优化GDTW-SVM的参数(K，τ)分别取(0．2，0．5)、(0．2，0．2)和(0．5，0．5)，分别重复分类识别10次且取10次识别结果的平均值作为使用该组参数的优化GDTW-SVM的识别结果，最终取三组识别结果中的最优识别结果作为优化GDTW-SVM的识别结果；以上实验中，γ=1．9。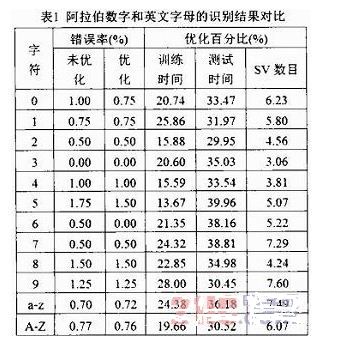

表1是阿拉伯数字和英文字母的识别结果对比。其中，英文字母数目较多，因此，仅给出平均识别结果。优化后的GDTW-SVM和未优化的GDTW-SVM的实验结果对比显示：参数k和τ的引入不仅使字符识别的错误率基本保持不变，同时，训练时间减少13～25％、测试时间减少29～39％、支持向量的数目也减少3．0～7．6％。

5 结论

本文提出了在GDTW核函数中引入参数k和τ，约束GDTW最优对齐路径的计算空间，然后构造GDTW-SVM分类器。实验结果表明，优化后的GDTW-SVM分类器的识别率与未优化的分类器的识别率基本相同；同时，支持向量数目减少，计算时间有13％～39％的减少，有利于GDTW-SVM分类器的联机手写识别的应用和推广。