基于DSP的SPWM直接面积等效算法的分析

时间：07-19 来源：点击：

变频技术作为现代电力电子的核心技术,集现代电子、信息和智能技术于一体。针对工频(我国为50 Hz)并非是所有用电设备的最佳工作频率，因而导致许多设备长期处于低效率、低功率因数运行的现状,变频控制提供了一种成熟、应用面广的高效节能新技术。
　　而SPWM（正弦波脉宽调制）波的产生和控制则是变频技术的核心之一。开始的SPWM生成技术是采用模拟电路构成三角波和正弦波发生电路，用比较器来确定他们的交点。这种方法电路复杂，精度较差，早已淘汰。后来人们采用单片机和微机生成SPWM波，但受硬件计算速度和算法计算量的影响，往往无法兼顾计算的精度和速度。再后来随着具有强大运算能力的DSP和一些新算法的出现，这一问题得到了较好地解决。
　　1 算法的原理
　　一般SPWM波形的产生有以下几种方法：自然采样法、规则采样法、低次谐波消去法直接面积等效法等。其中自然采样法的精度很高，但他求解导通关断点需要解一个超越方程，计算量很大，一般不被采用。低次谐波消去法计算复杂，只能用查表法，而且这种方法的波形频率和幅值是不可以连续变化的。因此将主要分析规则采样法，直接面积等效法这两种方法的原理。
　　规则采样法是从自然采样法演变而来的，他由经过采样的正弦波(实际上是阶梯波)与三角波相交，由交点得出脉冲宽度。这种方法只在三角波的顶点或底点位置对正弦波采样而形成阶梯波。其原理如图1(a)所示。
　　其中：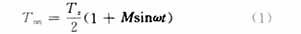
Tz: 三角载波周期
M: 调制深度(正弦波与三角波幅值比)
t：某采样时刻
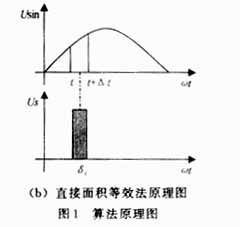
　　直接面积等效法的基本原理如图1(b)所示。
　　在图中的正弦半波波形中取一小区间［t，t+Δt］，其面积为S1，则与其面积相等的矩形脉冲面积为S2，宽度为δi。设正弦波幅值为Usin，调制度为M，矩形脉冲幅值为Us。有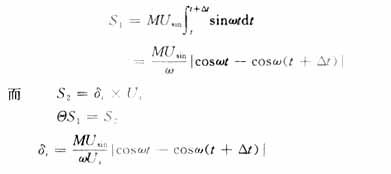

　　式中k代表第k次采样，N代表半周期内对正弦波的采样点。则IGBT的开关时间可如下计算：

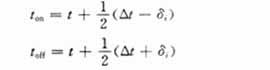
　　2 算法的分析及其在DSP上的实现
　　(1)算法的分析
　　在生成SPWM波形时，通常有查表和实时计算两种方法，实际使用时往往是两种方法的结合，即先离线进行必要的计算存入内存，运行时再进行较为简单的在线计算，这样既可保证快速性，又不会占用大量的内存。
　　规则采样法通常事先存入正弦函数表和不同载波频率时的Tz/2,运行时根据要求的Tz,M和ω即可算出开关器件的导通时间（详见公式1）。这种方法的计算量很小且波形的幅值和频率都是可以连续变化的。
　　直接面积等效法通常事先存入不同频率下的余弦函数表，运行时也只要进行简单的乘法和减法运算（详见公式2）。这种方法的计算量适中且波形的幅值和频率也是连续变化的。
　　由规则采样法的原理可知他是用一近似的阶梯波来代替正弦波与三角波进行比较，因此他的精度较低，但由于计算简单，在使用单片机和微机生成SPWM波的时代得到了较为广泛的应用。但随着具有强大运算能力的DSP的出现，使得兼顾计算的精度和速度这一问题有了解决的希望。因此采用具有较高精度且计算量适中的直接面积等效法和DSP相结合来解决这一问题。
　　(2)DSP的特点
　　DSP的厂家很多，国内应用主要以TI公司的居多。这里采用TI公司的TMS320系列。TI公司的TMS320C2000 DSP是基于320C2xLP核。为了实现小数的算术运算和验证小数的乘积，C2xLP的乘积寄存器的输出通过乘积移位器，以抑制运算中产生的多出来的Bit。该乘积定标移位器允许作128个乘积累加而不会产生溢出。基本的乘积累加（MAC）周期，包括将一个数据存储器的值乘以一个程序存储器的值，并将结果加给累加器。当C2000循环执行MAC，则程序计数器自动增量，并将程序总线释放给第二个操作数，从而达到单周期执行MAC。
　　C2000系列中的C24x系列的芯片具有事件管理器。该事件管理器具有3个加/减定时器和9个比较器，可以和波形产生逻辑配合产生12 PWM的输出。支持同步的和异步的PWM产生。他还支持一个空间向量PWM状态机，用开关功率晶体管来实现，以延长晶体管的寿命和降低功耗。一个关机段产生单元也有助于保护功率晶体管。其原理如图2所示。

　　可以看到，为了实现实时的变压与变频，需要根据当前载波所在时间T做大量的运算，而这些运算都要求在一个载波周期内完成。以载波频率为15625Hz为例，其周期为64μs，若要求三相输出，则所有这些运算都要求在32μs内完成。这对于单片机而言，是完全不可能的。而对于DSP而言，其指令周期为50ns，且多为单周期指令，并且有单周期的乘法指令。因此，充分利用了DSP的强大运算能力，才最终实现了上述计算的实时完成。

(3)直接面积等效法的

上一篇：基于DSP的多激光威胁信号分选和码型识别
下一篇：ARM-Linux平台下GPS信号的采集与处理研究

载波 DSP 周期单片机 SPWM 相关文章：

栏目分类