快速小波变换的定点DSP实现
小波变换具有良好的时--频局部性,是分析奇异信号的重要方法。定点DSP在工程中的应用十分普遍,具有低成本,高性能的特点。利用DSP实现小波变换可以满足工程是实时性的要求。文中简要介绍了小波变换理论及算法,并结合TI公司的16位定点DSP说明算法的实现。
关键词:快速算法 小波变换 DSP
1 引言
小波变换是近年来发展起来的一种数学理论和方法。作为一种新兴的理论,小波分析是数学发展史上的重要成果,对工程应用产生了深远的影响。广泛应用于语音信号处理、图像信号处理、信号检测、语音与图像编码、多尺度边缘提取与重建等领域。近年来,在电力系统中也开始应用小波分析进行故障检测及故障定位,并取得了有效的成果。
计算机只能处理数字信号,所以在实际信号处理中,常采用离散形式的小波变换(Discrete Wavelet Transform,DWT)。由于小波变换算法的复杂性,尽管当今处理器芯片运算速度得到了大幅度的提高,仍然在实时性上不能满足要求。为了简化计算过程,人们发展了一些快速算法,如Mallat塔式算法,及利用调频Z变换(chirped Z Transform,CZT),梅林变换(Mellia Transform)进行快速计算等算法。其中,尤其以Mallat塔式算法在实际应用比较广泛。
在数字信号处理领域,通常使用专用的数字信号处理器芯片(DSP)以完成特定的运算要求。美国TI公司是全球最大的DSP供应商,其生产的TMS320C2xx系列16位定点DSP芯片具有高性能、低价格等特点,具有广泛的应用领域。本文中用该系列DSP芯片实现小波变换的快速算法。
本文将小波变换快速算法用DSP加以实现,既可利用小波变换实现应用要求,又可降低成本,增强市场竞争力。尤其在当今,随着电力系统的不断发展,及用户对电能质量的要求越来越高,对电力系统运行监控及保护的采样点数越来越多的情况下,利用此方法可以解决运算量大、运算精度高的问题。
2 小波变换及算法
2.1 小波变换
小波函数的确切定义为:
设ψ(t)为-平方可积函数,若其傅里叶变换ψ(ω)满足条件
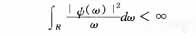
则称ψ(t)为一个基本小波或小波母函数。将其进行伸缩和平移后,得到小波基函数
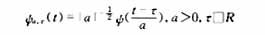
所谓小波变换就是把信号在上述小波基下进行展开。当然,此变换必须存在逆变换,否则,不能恢复原信号,该变换就没有什么意义了。
2.2 多分辨率分析
多分辨率分析在正交小波变换理论中具有非常重要的地位,在多分辨率分析理论产生之前,人们构造正交小波基函数要凭借技巧,具有一定的难度。自从有了多分辨率分析理论,这项工作变得容易的多。当然,要寻找合适的基函数还是需要一定的经验的。当找到了合适的滤波器系数后,就可以利用Mallat给出的快速小波算法来计算小波变换了。
通俗的讲,多分辨率分析就是把空间V0上的函数f(t)分解为细节部分W1(小波空间)和大尺度逼近部分V1(尺度空间),然后将大尺度逼近部分V1进一步分解,如此重复就可得到任意尺度(或分辨率)上的逼近部分和细节部分。
2.3 滤波器系数
根据多分辨率分析理论,如果φ(t),ψ(t)分别为尺度空间V0及小波空间W0的一个标准正交基函数,则在任意相邻尺度j,j-1之间,都有二尺度空间基函数关系
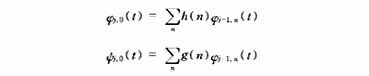
其中的h(n),g(n)即为滤波器系数,由尺度函数φ(t)和小波系数ψ(t)决定。
2.4 Mallat塔式算法
当有了一组小波基函数后,剩下的事就是计算分解了,即把信号用小波基函数表示出来,从而关键问题是求出表示式中的系数。根据多分辨率分析,将信号f(t)□Vj-1分解一次(即分别投影到Vj、Wj空间),此时cj,k和dj,k为j尺度上的展开系数,经过不算复杂的推导,可得
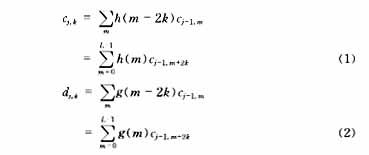
其中cj,k和dj,k分别称为j尺度空间的剩余系数和小波系数,上式说明它们可由j-1尺度空间的剩余系数cj-1,k经滤波器系数进行加权求和得到。实际中的滤波器h,g的长度都是有限长的或近似有限长的,因此分解运算非常简单。将cj,k进一步分解下去,可分别得到Vj+1、Wj+1空间的剩余系数Cj+1,k和小波系数dj+1,k
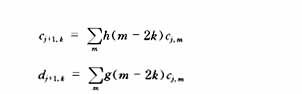
从而得到任意尺度空间上的分解。分解过程如图所示

在上述算法中必须要有一个初始输入序列Cj-1,k,分解才能顺利进行,这是一个问题。在大多数应用中,为了简便,常用输入信号的采样序列来近似作为C0,k。在一些文献里也给出了其它几种确定C0,k的方法。
3 算法在DSP上的实现
假设输入信号x(t),采样频率N(=2n),得采样序列x(k),k=0,…,N-1,作为初始输入序列C0,k。滤波器系数h(m),g(m),m=0,…,L-1。为了应用简便,(1)、(2)式可变为
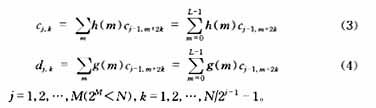
- 一种长序列小波变换快速算法的DSP实现(08-11)
- 一种基于TS201的归一化互相关快速算法(06-29)
- 单片机求平方根的高效快速算法(01-18)
- Cortex—M0单片机二-十进制整数转换的快速算法(08-31)
- 单片机开平方的快速算法(06-29)
