基于DSP和增量式PI电压环控制的逆变器研究

摘要：研究了一种基于数字控制的逆变器，该方案采用电压瞬时值环控制，以提高输出稳定性，同时兼顾输出动态性能。反馈电路中采用增量式PI法则，并对PI增量及PI输出进行限幅控制,避免因误扰动造成输出的不稳定，进一步确保系统的稳定性与动态性能。采用TMS320LF2407A来实现算法，并进行了一个输出最大值为200V，输出功率为500W的逆变器实验。

关键词：逆变器；电压环控制；增量式PI；DSP控制

0 引言

目前，逆变器应用最为广泛的PWM技术中，SPWM控制具有很多优点。其控制技术主要有电压瞬时值单环反馈、电流瞬时值单环反馈、电压电流双环反馈环控制及电压空间矢量控制。电压环使系统有较好的稳定性，瞬时值反馈则增强系统的动态性能[1]。电压环采用PI控制，其中比例环节及时反映控制系统的偏差信号，偏差一旦产生，控制器立即产生控制作用，以减少偏差；积分环节主要用于消除静差，提高系统的无差度。相对于位置式控制，增量式控制误动作影响小，必要时可以用逻辑判断的方法去掉；且手动/自动切换时冲击小，便于实现无扰动切换；同时其算式中不需要累加，比较容易通过加权处理而获得比较好的控制效果[2]。

相对于数字控制，传统的模拟控制已暴露诸多缺点：需要大量的分立元器件和电路板，制造成本比较高；大量的模拟元器件使其之间的连接相当复杂；模拟器件的老化问题和不可补偿的温漂问题，以及易受环境干扰等因素都会影响控制系统的长期稳定性。随着微处理器的可靠性与质量的不断提高，数字控制已经在逆变控制中占据着主导地位[3]，本文提出了一种基于DSP控制的方案。

1 逆变器建模

单相全桥逆变器如图1所示，E为输入直流电压，S₁～S₄为开关管，L为滤波电感，r为电感等效内阻，C为滤波电容，R为负载。

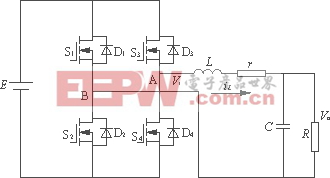
图1 单相全桥逆变器

将电感用L_s表示，电容用1/C_s表示，可推导出输出电压V_o（s）与AB两点间电压V_i（s）之间的传递函数G（s）如式（1）所示。

G（s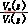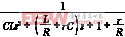）==（1）

忽略电感等效内阻，则式（1）可简化为

G（s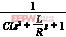）=（2）

在一个开关周期中，当S₁及S₄导通时，v_i为－E；当S₂及S₃导通时，v_i为E。由于开关频率与输出频率相比为400，故一个开关周期中可以用平均值代替瞬时值。

v_i=ED＋(－E)(1－D)=(2D－1)E（3）

本方案采用双极性SPWM，故

D=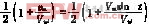（4）

式中：v_m为正弦波信号，v_m=V_msinωt；

V_tri为三角载波峰值。

则调制比M为

M=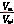（5）

将式（5）代入式（3）可得

v_i≈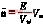（6）

转化为频域有

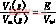（7）

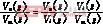
由式（7）与式（1）可得式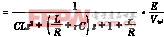（8）

（8）

此即逆变器输出传递函数，由此可得逆变器的等效框图如图2所示。

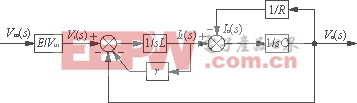
图2 逆变器等效框图

2 控制方案设计

本系统采用电压环反馈，为提高动态性能，采用瞬时值控制。电压环控制中，采用增量式PI控制，同时对其算法进行了优化，确保输出具有较好的稳定性。控制器采用TI公司的TMS320LF2407A，其最高工作频率可达40MHz，能够较好地实现以上算法。

2.1 电压环设计

忽略电感等效内阻，电压环等效框图如图3所示。

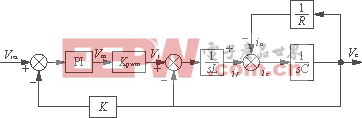
图3 电压环等效框图

图中：K_pwm为PWM环节等效增益，其大小为调制波到逆变器AB两端输出的增益；

K为反馈回路中的电压采样系数。

图3可简化为图4。

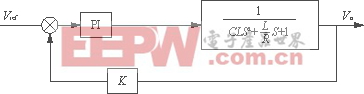
图4 电压环简化框图

图中K_pwm系数已归于PI模块中。逆变器开关频率取为20kHz，输出为工频，则取LC滤波器的转折频率f_n为1kHz，综合考虑电感电流纹波与压降，取L=1mH，C=10μF。本实验取满载时R=40Ω。

设PI环节传递函数为

G（s）=K_p＋（9）

则系统的开环传递函数为

G（s）=K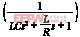（10）

取PI补偿频率为500Hz，而系统的穿越频率为1kHz。则由式（10）可得

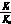=2π×500（11）

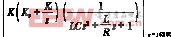=1（12）

式中：K为采样系数，实验中设计为0.014。

联立式（11）及式（12）可得

k_p=39 k_i=124416

其波特图如图5所示。

图5 电压环波特图

从图5中可以看出，系统相角裕度为60°，满足稳定性要求。图6为仿真所得的输出波形。

从图6中可看出，输出波形为正弦波，幅值为200V，频率为50Hz，与设计值相符。

图6 逆变输出波形

2.2 增量式PI算法及其优化

PI环节的传递函数为式（9），其对应的时域方程式为

y（t）=k_p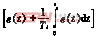（13）

式中：y（t）为PI输出；

e（t）为PI差动输入；

T_i为积分时间常数；

k_p为比例系数。

对式（13）离散化得

y_k=k_p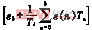（14）

式中：T_s为采样时间。

这即是位置式PI控制，而若采用增量式PI控制，可避免误动作，同时运算不需要累加，对数字控制尤其方便。由式（14）可得

y_k－1=k_p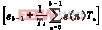（15）

由式（14）与（15）可得

y_k=y_k-1＋k_p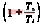e_k－k_p·e_k－1（16）

式（16）为一般的增