基于单片机的磁性编码器信号细分系统的设计

磁性编码器输出信号电子细分研究的现状和意义

在数字式传感器中，磁性编码器是近几年发展起来的一种新型电磁敏感元件。磁性编码器具有不易受尘埃和结露影响、结构简单紧凑、响应速度快（可达 500~700kHz），体积小巧等优点，同时利用磁性编码器可将多个元件精确地排列组合从而构成构成新功能器件和多功能器件。由于磁性编码器具有上述诸多优点，因而近年来在高精度测量和控制领域中的应用不断增加，作为一种重要工具，磁性编码器已成为必不可少的组成部分，其市场需求量每年以20%～30% 的速度增长。在高速度、高精度、小型化、长寿命的要求下，在激烈的市场竞争中，磁性编码器以其突出特点而独具优势，成为发展高技术产品的关键之一。在磁性编码器的研制生产方面，提高磁性编码器的分辨率和小型化现已成为各国研究发展的重点。

要提高编码器的分辨力必须增加其磁极数，一方面会增加传感器的成本，另一方面会因编码器体积的增大而影响其应用。因此对磁性编码器的输出信号进行二次细分就显得十分必要。

编码器信号信分的方案主要分为硬件细分和软件细分两类。硬件细分虽然可以得到较快的响应速度和实时输出的细分信号，但要实现较高的分辨率需要较高的成本。软件细分虽然在实时性存在一定缺陷，但可以在较小成本投入下获得较高的分辨率，并可以根据需要灵活设定分辨率。

本文将探讨利用成本较低的单片机系统实现磁性编码器信号细分的算法和实现信号实时输出的方案。本系统的设计思想是：根据两采样点之间的机械角度和细分精度计算出两个采样点之间应输出的脉冲的数目，并在系统的控制下输出，从而实现信号细分的目的。因此信号细分方案实际上是由旋转机械角度的计算和细分脉冲的输出控制两部分组成的。

旋转角度测量方案和硬件电路实现

系统中采用的磁性编码盘能够输出两路正交的正弦信号，编码器每旋转一周，可输出8个连续的正弦波。由于电机每旋转一周对应360度的机械角度，因此每个正弦波对应45度的机械角度，而每个正弦波又对应360度的电角度，因此正弦波90度的电角度的变化量对应磁性编码器11.25度机械角度的变化。

编码盘输出的是两路正交的正弦信号，而在正弦信号的一个单调区间中，信号的幅值和编码器的机械位置是一一对应的，于是可以通过测量信号的幅值转换成对应的角度信号，从而实现对磁编码信号的细分。

构造近似三角函数 ，构造函数的波形如图1所示。

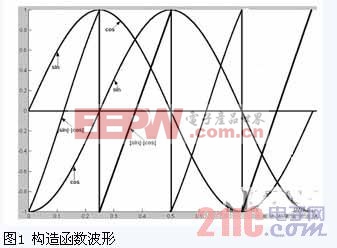
由波形图可以看出，新构造的函数以90度的电角度为周期（对应机械角度为11.25度）。如果相邻两采样点在一个周期内，则可按照公式计算编码器的机械位置；如果相邻两采样点不在一个周期内，则只需在式1的计算结果上加上N×11.25即可（N为两采样点之间的周期数）。采用这样的构造函数可以大大简化程序设计，从而提高系统的实时性。

电路结构框图

系统电路结构框图如图2所示。两路正弦信号通过编码电路生成与正弦波相对应的编码信号，CPU可以根据编码信号对信号的整数周期进行计数。

由编码器生成的编码信号控制多路开关实现两路输入信号之间的切换，以实现当 =N×90o（N=1，3，5，……）时互换两路输入信号的功能。采样保持器和A/D转换器在CPU的控制下，对同一时刻的两路正弦信号同时进行采样，并对采样保持器保持的信号进行A/D转换，转换后的数据经8255传输至CPU。

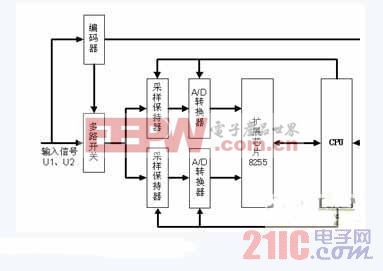
图2 信号细分硬件电路图

细分方案软件部分设计

电子细分方案软件流程图如图2所示。

在脉冲的输出控制上需要解决如下两个问题：如何输出细分脉冲以及如何控制细分脉冲的输出速率。

编码盘的转速变化是连续的，不会发生突变，因此可以近似认为在一段极短的时间内，电机的转速是恒定的，在此时间段内也就完全可以按照等时间间隔输出脉冲。假设电机的速度响应时间为100毫秒，在恒定加速度下达到1000转/分的转速，程序的执行周期为3000微秒，在一个程序周期中，按匀速处理产生的角度误差最大不超过0.27度，也就不会导致脉冲的误输出，完全可以保证精度要求。按照恒定速率在极短的时间内输出细分脉冲可以大大简化程序设计，并可以大幅度提高系统的实习响应性能。

由于细分脉冲数目必须要等到下一次采样完成后才能确定，因此脉冲的输出在时间上必然会滞后一个程序周期。如果设定程序执行周期为3毫秒，按编码盘每分钟旋转1000转，每转输出1000个细分脉冲计算，则输出信号最多会产生50个脉冲的滞后，相当于18o的机械角度误差。如果编码盘的转速增加，该误差会变得更大。同时，由于程序的执行周期不是一个固定值，因此由此所产生的信号滞后也将