基于PSD的微位移传感器建模的实现方法

位置敏感传感器(position sensitive detector，PSD)广泛应用于光学位置、角度的测量与控制、工业自动化生产、远程光学控制系统、微电子生产中的各类检测和监控、位移和振动监测等。在PSD的众多应用领域中，应用最为广泛的就是位移测量。本文通过光学三角测量的方法将测量物理位移信号转换成PSD能够测量的位移信号，然后利用PSD工作原理将位移信号转换成电流信号，通过后续电路将电流信号转换成电压信号，经过放大、滤波、A／D处理后交由计算机对采集得到的电压(V)和位移(S)信号进行处理。为准确反映该PSD的微位移传感器系统的V-S间关系，实现精确测量，需要拟合出一条曲线尽可能逼近PSD的微位移传感器实际的输入、输出特性。文中采用MATLAB语言，运用矩阵运算，由实验测得数据采用分段拟合的方法建立了PSD的微位移传感器V-S间的数学模型，对于PSD的微位移传感器实际的非线性特性进行拟合，逼近得出最佳关系曲线。

1 基于PSD的微位移传感器测量原理分析
1．1 PSD的工作原理
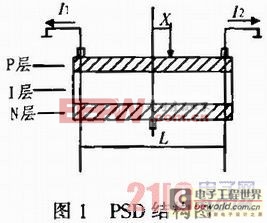
PSD分为一维PSD和二维PSD。一维PSD大致分为P-I-N 3层。一维PSD截面如图1所示。表面P层为感光面，从P层两侧分别引出一个电极，作为输出。中间的I层为电离层。底面N层的引出一个电极，作为公共端并施加反偏电压。PSD的光敏层接受入射光照射时，在相应的入射位置上所产生的电荷与光能成正比例关系，电荷定向移动形成光电流由P层两个输出电极输出。2个电极输出的电流大小都与入射光点位置到各电极之间距离有关，若感光面电阻是均匀分布的，距离越大，光电流越小；反之，则越大。

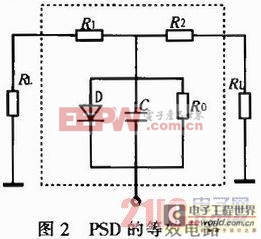
PSD的等效电路如图2所示，设电极1和电极2的距离为L，电极1和电极2输出的光电流分别为I1和I2，则电极3上的电流为总电流I0，并且IL=I1+I2。若以PSD的中心点位置作为原点，光点离中心点的距离为X。对一维PSD，如果负载电阻与面电阻相比很小，则有式(1)关系：

由式(1)可以看出光点坐标X仅和两极输出电流有关，而和入射光点强度无关，因此，若可以通过实验测量获得参数I1和I2的数值，光点坐标X就是可求的。

1．2 光学三角法构成的位移尺寸传感器
PSD进行位移测试时经常采用光学三角测量法。具体过程为：当激光束入射到被测试件表面时，会形成漫反射光斑，将其作为信号，利用透镜成像原理将收集到的漫反射光会聚到焦平面的光接收器上形成像点。当入射光斑随被测物面移动时，像点在光接收器上面做相应移动，根据像移大小和系统结构参数可以确定被测物面的位移量。基于PSD的微位移传感器测试原理由图3所示。

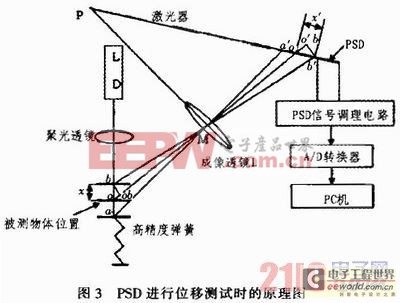
由于直接从电极输出的是微安级的光电流变化，并且负载电阻应该尽可能小，因此需要合适的信号调理电路对PSD的输出信号进行处理和运算才能得到位置坐标。本系统的PSD信号调理电路主要由前置放大器、加法器、减法器、除法器等构成。其中包含4个高精度运算放大器。两个作为前置放大运算放大器，将电流信号转换成电压信号进行放大，放大倍数取决于反馈电阻阻值。本系统在调试时为了提高测量精确度采用了精确阻值的电阻。另外两个高精度运算放大器分别作为加法器和减法器，为了实现精确测量，尽可能避免软件方法实现的除法器在两路数据采集过程中难以真正实时同步的缺点，本系统采用高精度模拟除法器实现除法运算功能。由于加法器、减法器、除法器的输出具有一定的电压波动，所以系统还加入了滤波器。用数据采集卡PCL-818HD采集高精度模拟除法器的输出电压并实现A／D转换，通过编程实现转换结果和PC机中的MATLAB数据连接，通过调用自行编写的建模程序实现对基于PSD的微位移传感器的建模，即在传感器系统中，电压大小与光点位置和原点之间的距离近似成线性比例关系。

2 用MATLAB语言建立数学模型原理
实验过程中所得到的实验数据往往是离散的，传感器建模的最终目标是通过某些拟合方法得到输入量与输出量之间的连续光滑曲线。实际测得一组传感器测量数据集{Xk，Yk}，(k=1，2，…n)，其中Xk为被测量，Yk为传感器输出量。基于最小二乘法的传感器数学模型的建立，就是要用多项式(2)

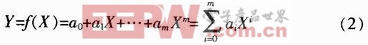
拟合测量数据集{Xk，Yk}，(k=1，2，…n)，使φ值最小。一般均采用欧氏范数‖δ‖2作为误差度量的标准。使用MATLAB的M语言对最小二乘算法进行编程，通常采用两种方法：利用polyfit函数进行多项式拟合，或利用矩阵除法解决复杂函数的拟合。文中用第一种方法拟合基于PSD的微位移传感器的数学模型。函数polyfit的输入量为X、Y、n，其中X、Y即为需要建立相互关系的2个变量的测量值，以数组的形式输入，n为多项式的阶数，输出的是多项式系数的行向量，得到的多项式是降幂的。对给定的一组数据(Si，Vi)(i=0，1，…，n)，选取线性无关的基函数φ={S0，S1，…，Sm}，要求由φ中找出一个函数y=V*(S)，使误差平方和