基于ARM的过采样技术
过采样技术是提高测控系统分辨率的常用方法,已经被广泛应用于各个领域。例如,过采样成功抑制了多用户CDMA系统中相互正交用户码接收机(A Mutually Orthogonal Usercode-Receiver,AMOUR)的噪声[5~6],提高了光流估计(optical flow estimation,OFE)的精度[7],改善了正交频分复用(OFDM)信号的峰-均比[8]等。但是,这些过采样技术应用的前提是采样前的信号幅值能与ADC的输入范围相当。而用ADC采集微弱信号时,直接使用过采样技术提高不了精度,而且由于信号幅值远小于ADC的输入范围,它的有效位数还会减小,使精度随之下降。本文采用先叠加成形函数的方法,然后利用过采样技术,解决了因为信号幅值小,而使过采样失效的问题。本文还详细分析了成形函数类型和幅值,以及过采样率对分辨率的影响。
1 过采样技术分析
1.1 过采样原理
过采样是对待测数据进行多次采样,获取样本数据,累计求和这些样本数据,并对它们均值滤波,减小噪声后最终获得采样结果。过采样在一定条件下能够提高信噪比(SNR),同时使噪声减弱,从而提升测量分辨率。过采样技术将采样频率提高到被采样频率的4倍,能过滤掉高于3fb的分量,用数字滤波器过滤fb~3fb的分量,最终有用分量被完全保存下来。若采取足够多次采样,则能重现原始信号。式(1)是过采样的频率要求

式(1)中,Fo为过采样频率;n为希望增加的分辨率位数;fb为初始采样频率要求。
1.2 过采样与噪声、分辨率的关系
在提出过采样与噪声的对应关系之前,对量化噪声作一简单描述。量化误差是由相邻ADC码的间距所决定,因此相邻ADC码之间的距离为

式(2)中,N为ADC码的位数;Vr为基准电压。式(3)为量化误差ed的关系式。
奈奎斯特定理指出,如果被测信号的频带宽度小于采样频率的1/2,那么可以重建此信号。现用白噪声近似描绘实际信号中的噪声,在信号频带中的噪声能量谱密度为

式(4)中,e(f)为带内能量谱密度;ea为平均噪声功率;fs为采样频率。
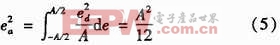
ADC量化噪声的功率关系如式(5)所示。由于量化噪声会引发固定噪声功率,因此针对增加的有效位数能够计算过采样比

式(6)中P为过采样比;fs为采样频率;fm为输入信号最高频率。低通滤波器输出端的带内噪声功率见式(7)。其中n2是滤波器输出的噪声功率
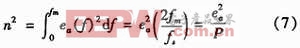
由此可见,过采样能减少噪声功率却又对信号功率不产生影响,在减小量化误差的同时,能够获得与高分辨率ADC相同的信噪比,从而增加被测数据的有效位数。通过提高采样频率或过采样比可提高ADC有效分辨率。
2 过采样满足条件及操作步骤
对于过采样,理论上需要信号有一定噪声,并且必须近似白噪声,幅度足够大。若噪声信号不能满足前面讲述的理论要求,就需要引入噪声激励。因此,选用周期性噪声作为激励信号。同时对激励噪声有一定要求:激励噪声幅度≥1 LSB;噪声均值在添加激励噪声时必须是0.
在理解过采样理论及需要满足的条件后,出于对具体应用的考虑,设计了过采样的操作步骤,概括如下:
(1)判断被采样信号是否有噪声,如果没有噪声,则叠加周期性激励噪声。
(2)对信号进行4n次过采样(n为希望增加的分辨率位数)。如果使用片内10位ADC,希望得到14位的ADC精度,则需要44即256次10位的过采样。
(3)抽取数字序列,对各个采样值进行累加。
(4)对累加后的采样数据,若提高n位精度则右移n位,最终得到过采样值。
3 LM
- Linux嵌入式系统开发平台选型探讨(11-09)
- 基于ARM体系的嵌入式系统BSP的程序设计方案(04-11)
- 在Ubuntu上建立Arm Linux 开发环境(04-23)
- 达芬奇数字媒体片上系统的架构和Linux启动过程(06-02)
- SQLite嵌入式数据库系统的研究与实现(02-20)
- 革新2410D开发板试用手记(04-21)
