6自由度机器人关节间隙误差分析及仿真

引言

深圳市众为兴数控技术有限公司自主研发设计的mr601机器人，是一款集工业教学应用于一体的min i型6自由度机器人，如图1所示，对应连杆坐标系见图2。



图1 mr601机器人



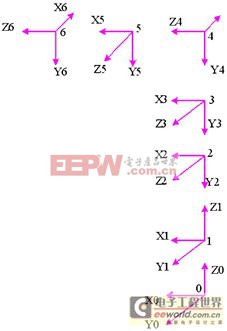
图2 机器人坐标系

该机器人采用基于pc的开放式控制系统，控制系统如图3所示。



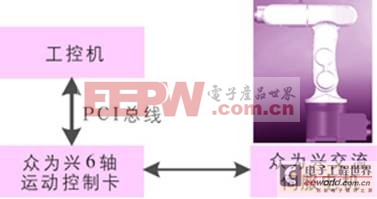
图3 mr601机器人控制系统架构

控制系统软件采用vc6.0开发，具有点位、空间直线、空间曲线运动功能，可以实现关节坐标编程和空间直角坐标编程，空间直角坐标与关节坐标相互转换。

轨迹试验

现让机器人绘制一正方形，以验证机器人整体性能。

机器人末端固定一黑色油性笔，工作平台上放置一白色带灰色条纹瓷砖，见图4所示，以便于机器人在其上绘图。



图4 机器人轨迹试验图

机器人末端姿态采用zyz欧拉角表示，单位为度；坐标单位为毫米，在直角坐标空间对机器人末端执行器坐标设置如下：

第一点：坐标(350,0,5)，姿态(0,180,0)；

第二点：坐标(450,0,5)，姿态(0,180,0)；

第三点：坐标(450,100,5)，姿态(0,180,0)；

第四点：坐标(350,100,5)，姿态(0,180,0)；

第五点：坐标(350,0,5)，姿态(0,180,0)；

其中，第一点与第五点重合以保证绘制出一封闭正方形。

将直角空间坐标转换为关节空间坐标。机器人根据生成的关节坐标进行正方形绘制。各点位置以及绘制结果如图5所示。



图5 机器人绘制轨迹图

结果显示，机器人所绘制轨迹为一平形四边形，存在以下问题：

● 第1点与实际点偏移2mm；

● 边12和边34与期望轨迹夹角为2°；

● 边23和边41与期望轨迹有近1度偏移；

● 轨迹线条不均匀。

误差分析

机器人的结构设计与装配对整体的性能影响很大，在对程序、电器部分排查后，将误差的原因锁定在结构部分。

机器人第一关节电机安装在基座上，其余5个关节电机安装在同一个方向，见图2坐标系x0y0z0中x0负向，重量集中在该方向。

用手晃动每个关节，发现第二关节(见图2 坐标系x2y2z2)存在关节间隙，该间隙主要是轴承轴向间隙引起。初步判断机器人轨迹偏移可能是由于第2个关节的间隙产生，机器人手臂重量导致手臂向间隙方向有一定角度的滚翻，即绕x0轴逆时针转动一微小角度。

建模仿真

现增加一虚拟关节，等效机械手臂的滚翻。虚拟关节轴线垂直于第2关节的轴线方向，建立图6所示的相关机器人坐标系。



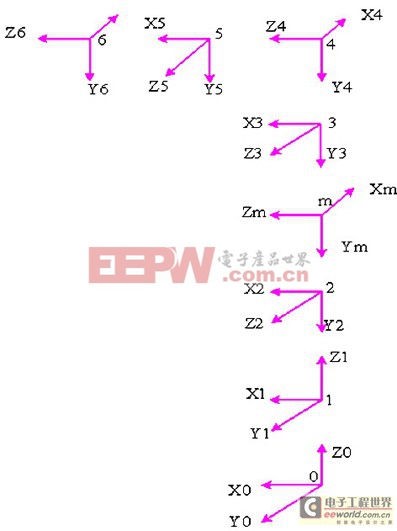
图6 增加虚拟关节机器人坐标系

其中：z0为基座原点，坐标系x2y2z2为机器人第2关节坐标系，坐标系xmymzm为增加的机器人虚拟关节坐标系，轴线zm垂直于关节2轴线z2。

根据图6的坐标系建立机器人空间运动方程。根据边线12和边线34的偏移角度，假定虚拟关节旋转2度，其状态在运动过程中不发生变化。进行matlab动态仿真，仿真结果如图7。



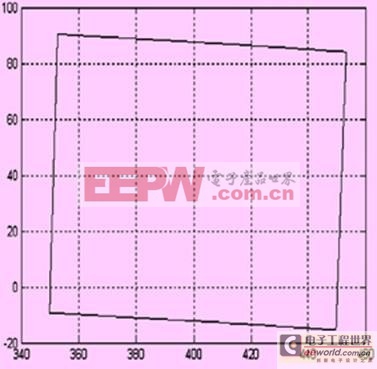
图7 仿真轨迹图

由图7的仿真图与图5的实际轨迹图对比可知，两者的轨迹走向基本一致；从图8的z向误差图可以得知，机械间隙导致z向有近0.1mm的变化。



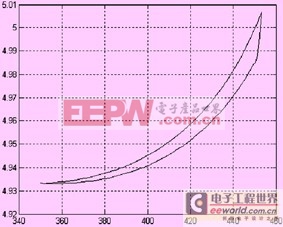
图8 轨迹z向误差图

由仿真分析结果可以断定，轨迹偏移主要由第2关节的轴承间隙引起。
从直观角度分析：
● 关节间隙导致机器人手臂有一定范围的滚翻，翻滚角度不变，随着手臂的展开偏移误差不断增大，导致边线倾斜。

● z向误差导致笔尖上下移动，线条轨迹不均匀。

结语

本方法将关节间隙等效为一个旋转一定角度的虚拟关节，在定性分析的同时，得到关节间隙对机器人精度的量化误差。

根据建立的误差方程求解机器人的逆解，部分关节轨迹为复数解。说明通过算法对于该误差的补偿很有限，机器人整体机械结构是决定机器人精度的关键因素。

对第2关节的轴承进行调整，轨迹偏移问题得到解决，可以绘制出规则的图形。