基于FDATool的FIR滤波器设计方法（一）

coe_9 = -650

coe_10 = -1241

数据输入时打了一拍，输出时打了一拍。综合后结果如下：

Number of Slice Registers： 2

Number of Slice LUTs： 19

Number of DSP48E1s： 11

关键路径中数据路径延时报告如图2所示，数据路径延时包括乘法器延时Tdspcko PCOUT AREG MULT (3.001ns)+ 10个级联加法器延时Tdspdo PCIN PCOUT(1.219)，数据路径延时总共15.017ns，因此fmax最大不过66.273MHz。可以发现综合器自动将乘法器和加法器在 DSP48E1中实现。

图2

加法树实现：

直接型FIR滤波器的一般实现方法关键路径中有较多级的加法器，所有加法器延时累加后导致关键路径延时较大，对整个FIR滤波器的性能造成了很大影响。为了解决加法器延时累加的问题，可采用加法树结构，如图3所示为采用了加法数的直接型FIR滤波器结构，这种层次化的树型结构，使加法器逻辑由级联结构转化成并行结构，这样整个路径的延时减小。

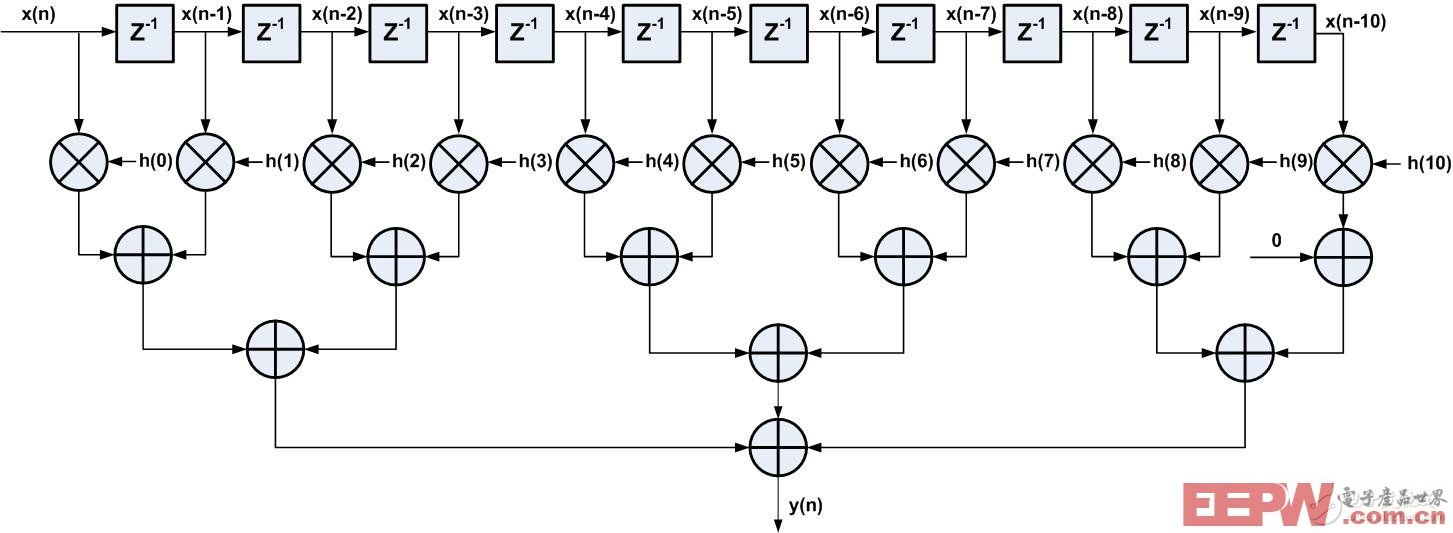
图3

流水线实现：

虽然直接型FIR滤波器采用加法树结构后优化了关键路径，但是时序还是不够理想，因为关键路径上至少有一个乘法器和一个加法器的延时，如果想竟可能的优化时序，可以分隔乘法器和加法器逻辑，中间加一级寄存器，即采用流水线实现。

那如何有效地分割逻辑呢?可以在图3中加法树结构的基础上分割，在原先的关键路径上，乘法器延时3.001ns，加法器延时1.219ns，因此可以将逻辑分割成如下**：

第1级：乘法器

第2级：2级加法器

第3级：3个数累加即2级加法器

如图4所示为流水线实现的FIR滤波器，逻辑分割后的关键路径是乘法器那一级，理论分析得到的延时只有3.001ns，如果时钟约束到250MHz可满足时序要求。

图4

实际得到综合结果如下：

Number of Slice Registers： 105

Number of Slice LUTs： 124

Number of DSP48E1s： 11

Minimum period： 3.037ns{1} (Maximum frequency： 329.272MHz)

fmax能达到329.272MHz，延时基本与预期的差不多，FIR滤波器能达到这样的性能基本能满足大多数应用了。

线性相位FIR滤波器：

FIR滤波器有一特征：线性相位，直接表现在抽头系数上，抽头系数为偶对称或者奇对称，在这节实例中，系数是偶对称的，即 h(0)=h(10)，h(1)=h(9)，h(2)=h(8)，h(3)=h(7)，h(4)=h(6)，直接型FIR结构优化后如图5所示，输入数据在与系数相乘之前，因系数对称，可以先将相同系数对应的数据进行预加操作，然后再与系数相乘，如此做法的好处是是乘法器资源减少了近一半，此例中DSP资源由原先需要11个到现在只需6个。而且，在Xilinx FPGA中的DSP48E1资源专门为线性相位FIR滤波器应用提供了预加pre-adder结构，即预加和乘法都可以在1个DSP48E1中完成，这样大大缩短了数据路径的延时，有利于时序收敛。

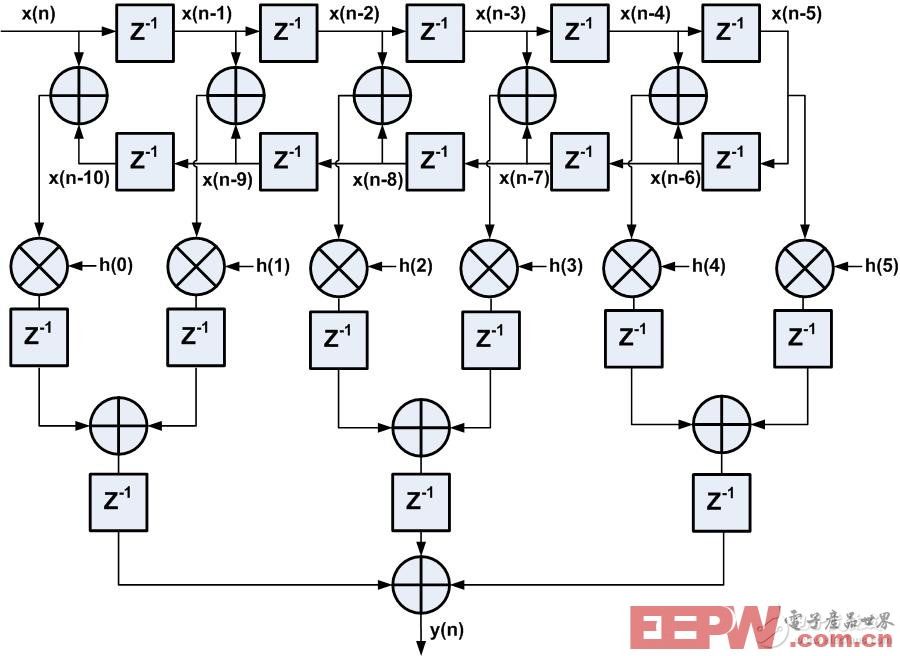
图5

实际得到综合结果如下：

Number of Slice Registers： 184

Number of Slice LUTs： 173

Number of DSP48E1s： 6

Minimum period： 2.854ns{1} (Maximum frequency： 350.385MHz)

fmax能达到350.385MHz，由于采用了加法树结构，避免了加法器级联延时，并且分了3级流水线实现。关键路径数据延时报告如图6所示，路径是从 DSP48E1输出端到dout_d，但是光从代码中看DSP48E1端到dout_d中间应该还有一级加法器的寄存，原来这个加法器采用了 DSP48E1中的累加器实现了。

图6