一种CORDIC协处理器核的设计与实现

图3所示。

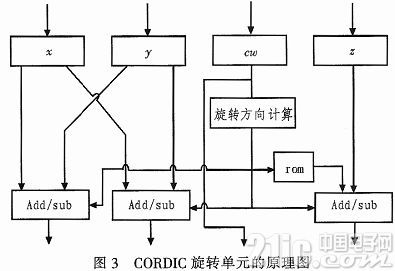
此模块首先通过控制命令字、yz分量计算出旋转的方向，然后对向量作旋转。由于圆坐标和双曲坐标模式下旋转的角度不同，所以需要根据控制命令字进行选择。由于使用了流水线结构，移位操作实际上通过布线而静态确定，不需要专门的移位器。模块使用3个可进行加减运算的ALU单元分别对xyz分量进行修正。Rom存储了圆坐标和双曲坐标模式下的旋转角度，其精度根据IP核的配置而定，可以简单地通过在实例化Verilog模块时指定参数来进行配置。

2.4 后处理单元

由图2可知，旋转单元的输出结果并不直接对应CORDIC协处理器所提供的函数。后处理单元对CORDIC旋转单元的输出结果进行处理，实现所需要的函数。具体的处理如表2所示。

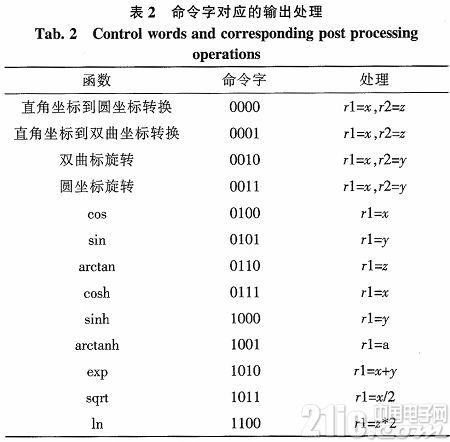
此外，由于前处理单元对圆坐标输入进行了象限折叠，后处理单元需要进行相应的修正。例如对于圆坐标旋转模式，如果输入的z∈[π/4，π/2]，则前处理单元会将z变为π/2-z，于是相应的后处理单元需要将x和y的值相交换。

2.5 补偿单元

由(4)可知，CORDIC每次旋转都会改变向量的模，故需要对最终的xy分量进行补偿。由于向量模变化只与坐标系模式有关，故补偿单元可以用一个常数乘法器实现。常数乘法器可以通过用华莱士树把移位后几个向量相加来实现。本文在线下通过程序穷举找出了一组加减操作数最少乘数编码方式，对于18位的配置，可以使用一个9输入的华莱士树和一个加法器实现，这使得该核在缺乏硬件乘法器的基于flash的Actel FPGA上也可以轻松使用。华莱士树中一位的结构如图4所示。

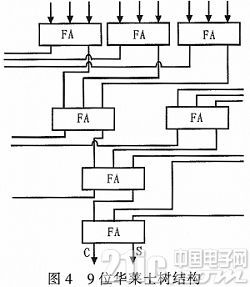
3 性能分析

为了证明所提出的IP核的实用性，本文选取了迭代次数16—20、扩展位数为5位的几种配置进行了综合。综合平台使用了航天电子系统常用的2种FPGA：A3P3000E和xc4vf40 综合结果如表3所示。

可见本IP核具有较高的性能和较低的资源占用率，可以较容易地被集成，且随着迭代次数和精度的提高，资源的增长趋势稳定，速度的下降并不明显。

一直以来有很多为加速CORDIC运算而提出的方法，其中很多使用了冗余数，试图通过冗余数进位传播有限的特点来降低加法器的延迟。但本文通过对比发现，基于冗余数的算法仅在A3P3000E的实现上有一定速度优势，而在virtex4上没有速度优势，还在资源利用率上有很大劣势。原因是当前的大多数FPGA针对常见运算逻辑，如加法器的实现作出了特殊优化，使用了快速进位链降低加法器的进位延迟。相对的，由于FPGA缺乏对冗余数逻辑的支持，冗余数加法器需要由基本单元综合生成，具有较大的布线延迟，且需要消耗大量的LUT或逻辑门资源。此外，由于冗余数使用2倍于补码长度的编码方式来表示数值，冗余数需要使用更多的寄存器寄存每级流水线的中间结果。综上，对于有效位数较少的配置，本文提出的CORDIC协处理器具有更好的性能与资源利用更具优势。

4 精度与误差

根据参考文献可知，CORDIC计算的误差主要来自2部分：由于每次迭代时用来修正z分量的角度有限而产生的近似误差和由于计算位数有限而产生的xy分量截断误差。为了尽量降低误差，首先应该保证旋转过程中用来修正z的数值是经过舍入得到的，而不是简单通过截断得到的，这样可以减小由于使用近似的旋转角度而产生的舍入误差。其次可以考虑在最终阶段运算结果前进行舍入。运算结果的舍入可以在补偿单元通过增加华莱士树的输入实现。即增加一个输入变量，其大小为最低有效位的一半，符号与补偿单元的输入相同。除此之外，需要根据所需的精度合理选择CORDIC协处理器的数据位数，增加扩展位，即对于n位的CORDIC运算，在迭代运算时使用n+m位，在迭代结束后舍弃m位，这样做可以保证前面的n位不受到截断误差的影响。本文选取了18位CORDIC来说明扩展位和迭代次数对精度的影响。对于圆坐标旋转模式，输入向量为x=2.0，y=0.0，z∈[-π，π]的所有可能输入向量;对于圆坐标向量模式，输入为模为2.0，夹角属于[-π，π]的所有可能输入向量;对于双曲旋转模式，输入为x=2.0，y=0.0，z∈[-1.0，1.0]的所有可能输入向量;对于双曲向量模式，输入为x=a+1，y=a-1，α∈[0.25，1.0]的所有可能输入。各个函数的误差与所选取的迭代次数和扩展位的关系如表4所示。

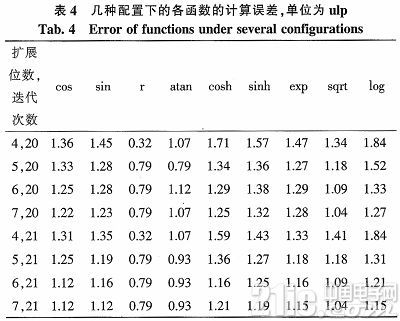
其中ulp为最低位单位。对于20位定点数有1ulp=2-18。配置为扩展位数和迭代次数。通过实验可以发现，对扩展后的向量进行截断会带来显著的误差增长。并且只会在使用较长扩展位时对结果进行舍入才有明显的效果，因为扩展位较少的情况下舍入反而可能会让结果向错误的方向舍入。最后值得注意的是双曲模式下的函数误差高于圆坐标模式