和顺序栈相类似，在队列的顺序存储结构中，除了用一组地址连续的存储单元依次存放从队列头到队列尾的元素之外，尚需附设两个指针front和rear分别之时队列头元素和队列尾元素的位置。为了在C语言中描述方便起见，在此我们约定：初始化建空队列时，令front=rear=0，每当插入新的队列尾元素时，“尾指针增1”；每当删除队列头元素时，“头指针增1”。因此，在非空队列中，头指针始终指向队列头元素，而尾指针始终指向队列尾元素的下一个位置。如图4所示。
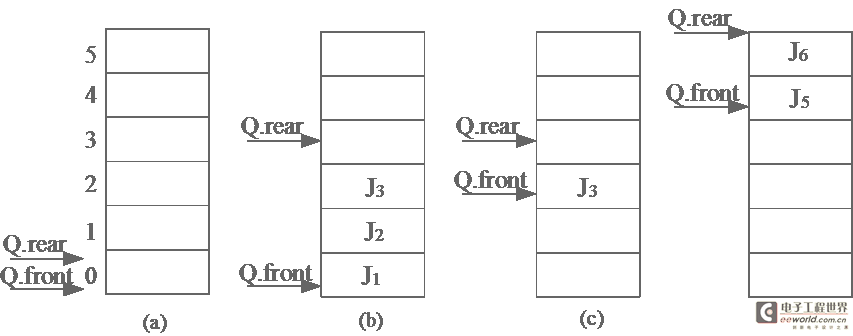图4 头、尾指针和队列中元素之间的关系
(a)空队列；(b)J1、J2和J3相继入队列；(c)J1和J2相继被删除；(d)J4、J5和J6相继插入队列之后J3及J4被删除
假设当前为队列分配的最大空间为6，则当队列处于图4(d)的状态时不可再继续插入新的队尾元素，否则会因数组越界而遭致程序代码被破坏。然而此时又不宜如顺序栈那样，进行存储再分配扩大数组空间，因为队列的实际可用空间并未占满。一个较巧妙的办法是将顺序队列臆造为一个环状的空间，如图5所示，称之为循环队列。指针和队列元素之间关系不变，如图6(a)所示循环队列中，队列头元素时J3，队列尾元素是J5，之后J6、J7和J8相继插入，则队列空间均被占满，如图6(b)所示，此时Q.front=Q.rear；反之，若J3、J4和J5相继从图6(a)的队列中删除，使队列呈“空”的状态，如图6(c)所示。此时亦存在关系式Q.front=Q.rear，由此可见，只凭等式Q.front=Q.rear无法判别队列空间是“空”还是“满”。可由两种处理方法：其一是另设一个标志位以区别队列是“空”还是“满”；其二是少用一个元素空间，约定以“队列头指针在队列尾指针的下一位置（指环状的下一位置）上”作为队列呈“满”状态的标志。
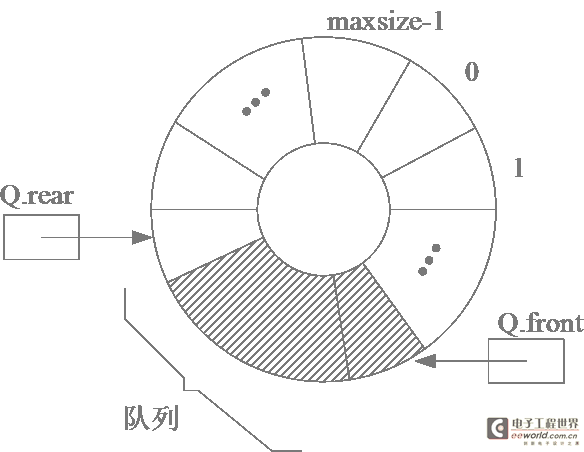
图5 循环队列示意图
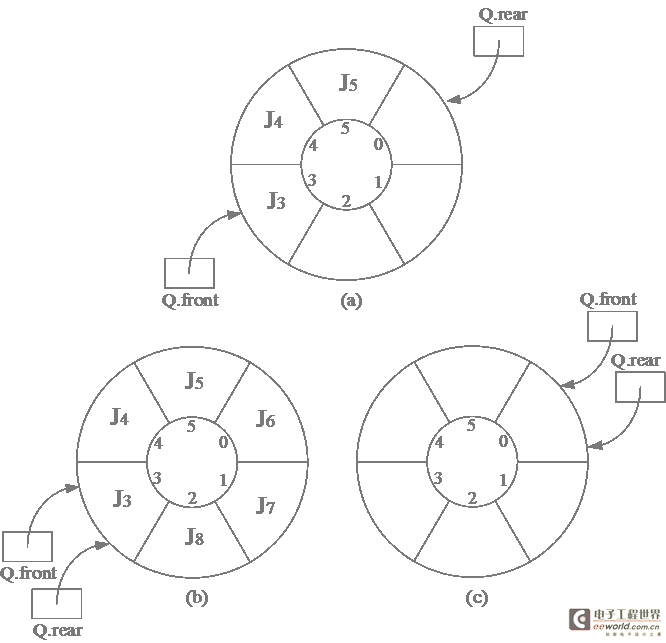
图6 循环队列的头尾指针 (a)一般情况；(b)队列满时；(c)空队列；
从上述分析可见，在C语言中不能用动态分配的一维数组来实现循环队列。如果用户的应用程序中设有循环队列，则必须为它设定一个最大队列长度；若用户无法预估所用队列的最大长度，则宜采用链队列。循环队列类型的模块说明如下：
//-----循环队列———队列的顺序存储结构-----
#define MAXQSIZE 100//最大队列长度
typedef struct{
QElemType *base;//初始化的动态非配存储空间
int front;//头指针，若队列不空，指向队列的头元素
int rear;//尾指针，若队列不空，指向队列尾元素的下一个位置
}SqQueue;
//-----循环队列的基本操作的算法描述-----
Status InitQueue(SqQueue &Q){
//构造一个空队列Q
Q.base=(ElemType *)malloc(MAXQSIZE*sizeof(ElemType));
if(!Q.base) exit (OVERFLOW);// 存储分配失败
Q.front=Q.rear=0;
return OK;
}
int QueueLength(SqQueue Q){
//返回Q的元素个数，即队列的长度
return (Q.rear-Q.front+MAXQSIZE) % MAXQSIZE;
}
Status EnQueue(SqQueue &Q, QElemType e){
//插入元素e为Q的新的队尾元素
if((Q.rear+1) % MAXQSIZE == Q.front) return ERROR;// 队列满
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1) % MAXQSIZE;
return OK;
}
Status DeQueue(SqQueue &Q, QElemType &e){
//若队列不空，则删除Q的对头元素，用e返回其值，并返回OK；
//否则返回ERROR
if(Q.front==Q.rear)return ERROR;
e=Q.base[Q.front];
Q.front=(Q.front+1) % MAXQSIZE;
return OK;
}
|
