浅谈DDS的原理、混叠及幅度调制

DDS架构基本原理

随着数字技术在仪器仪表和通信系统中的广泛使用，可从参考频率源产生多个频率的数字控制方法诞生了，即直接数字频率合成(DDS)。其基本架构如图1所示。该简化模型采用一个稳定时钟来驱动存储正弦波(或其它任意波形)一个或多个整数周期的可编程只读存储器(PROM)。随着地址计数器逐步执行每个存储器位置，每个位置相应的信号数字幅度会驱动DAC，进而产生模拟输出信号。最终模拟输出信号的频谱纯度主要取决于DAC。相位噪声主要来自参考时钟。

DDS是一种采样数据系统，因此必须考虑所有与采样相关的问题，包括量化噪声、混叠、滤波等。例如，DAC输出频率的高阶谐波会折回奈奎斯特带宽，因而不可滤波，而基于PLL的合成器的高阶谐波则可以滤波。此外，还有其它几种因素需要考虑，稍后将会讨论。

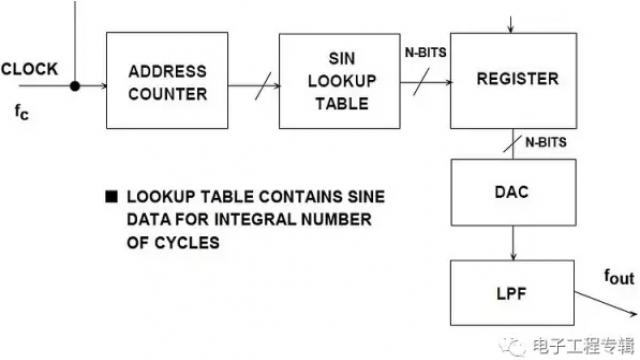
图1：直接数字频率合成系统的基本原理

这种简单DDS系统的基本问题在于，最终输出频率只能通过改变参考时钟频率或对PROM重新编程来实现，非常不灵活。实际DDS系统采用更加灵活有效的方式来实现这一功能，即采用名为数控振荡器(NCO)的数字硬件。图2所示为该系统的框图。

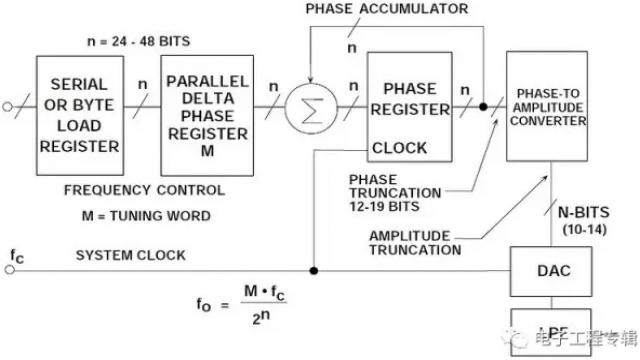
图2：灵活的DDS系统

系统的核心是相位累加器，其内容会在每个时钟周期更新。相位累加器每次更新时，存储在△相位寄存器中的数字字M就会累加至相位寄存器中的数字。假设△相位寄存器中的数字为00...01，相位累加器中的初始内容为00...00。相位累加器每个时钟周期都会按00...01更新。如果累加器为32位宽，则在相位累加器返回至00...00前需要232(超过40亿)个时钟周期，周期会不断重复。

相位累加器的截断输出用作正弦(或余弦)查找表的地址。查找表中的每个地址均对应正弦波的从0°到360°的一个相位点。查找表包括一个完整正弦波周期的相应数字幅度信息。(实际上，只需要90°的数据，因为两个MSB中包含了正交数据)。因此，查找表可将相位累加器的相位信息映射至数字幅度字，进而驱动DAC。图3用图形化的"相位轮"显示了这一情况。

考虑n = 32，M = 1的情况。相位累加器会逐步执行232个可能的输出中的每一个，直至溢出并重新开始。相应的输出正弦波频率等于输入时钟频率232分频。若M=2，相位累加器寄存器就会以两倍的速度"滚动"计算，输出频率也会增加一倍。以上内容可总结如下：

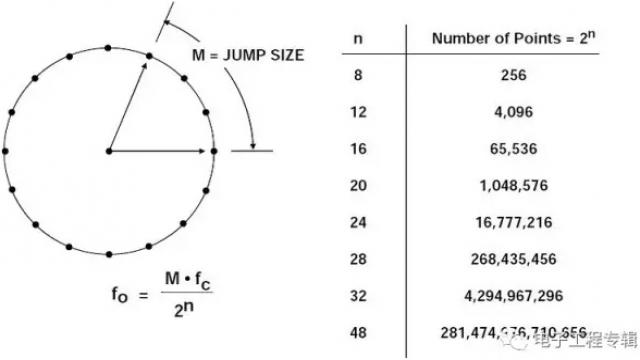
图3：数字相位轮

n位相位累加器(大多数DDS系统中，n的范围通常为24至32)存在2n个可能的相位点。△相位寄存器中的数字字M代表相位累加器每个时钟周期增加的数量。如果时钟频率为fc，则输出正弦波频率计算公式为：

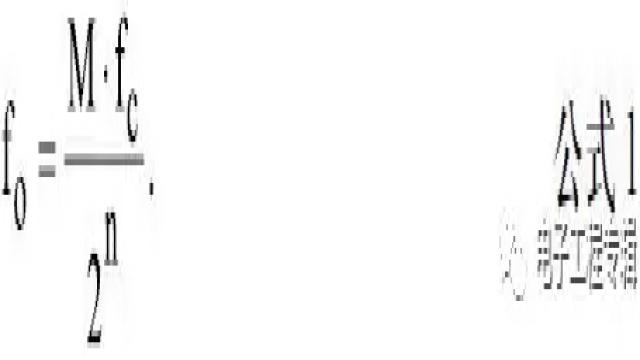
该公式称为DDS"调谐公式"。注意，系统的频率分辨率等于fc/2n。n = 32时，分辨率超过40亿分之一！在实际DDS系统中，溢出相位寄存器的位不会进入查找表，而是会被截断，只留下前13至15个MSB。这样可以减小查找表的大小，而且不会影响频率分辨率。相位截断只会给最终输出增加少量可接受的相位噪声。(参见图4)。

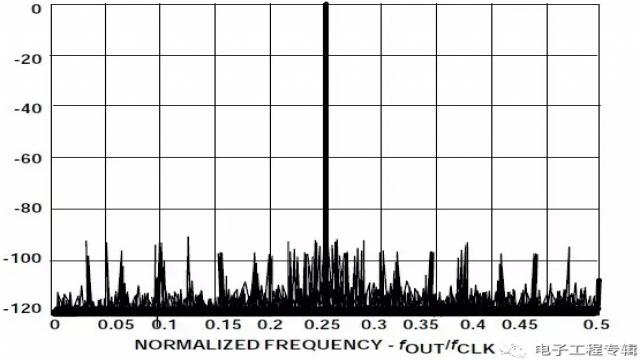
图4：计算得出的输出频谱显示15位相位截断时90 dB SFDR

DAC的分辨率通常比查找表的宽度少2至4位。即便是完美的N位DAC，也会增加输出的量化噪声。图4显示的是32位相位累加器15位相位截断时计算得出的输出频谱。选择M值后，输出频率会从0.25倍时钟频率开始稍有偏移。注意，相位截断和有限DAC分辨率产生的杂散都至少比满量程输出低90 dB。这一性能远远超出了任何商用12位DAC，足以满足大多数应用的需求。

上述基本DDS系统极为灵活，且具有高分辨率。只需改变M寄存器的内容，频率就可以立即改变，不会出现相位不连续。但是，实际DDS系统首先需要执行串行或字节加载序列，以将新的频率字载入内部缓冲寄存器，然后再载入M寄存器。这样就可以尽可能减少封装引脚数。新的频率字载入缓冲寄存器后，并行输出△相位寄存器就会同步操作，从而同时改变所有位。加载△相位缓冲寄存器所需的时钟周期数决定了输出频率的最大改变速率。

DDS系统中的混叠

简单DDS系统中可能会产生一种重要的输出频率范围限制。奈奎斯特准则表明，时钟频率(采样速率)必须至少为输出频率的两倍。实际最高输出频率限制在约1/3时钟频率范围内。图5所示为DDS系统中的DAC输出，其中输出频率为30 MHz，时钟频率为100 MHz。如图所示，重构DAC后必须跟随一个抗混叠滤波器，以消除较低的图像频率(100 –30 = 70 MHz)。

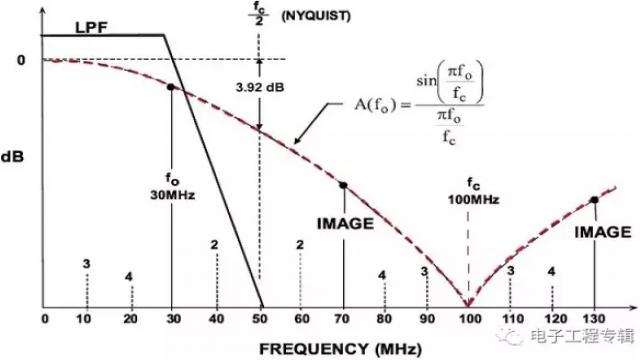
图5：DDS系统中的混叠

注意，DAC输出(滤波前)的幅度响应跟随着一个sin(x)/x响应，在时钟频率及其整数倍时，该值为零。归一化