基于电涡流传感器的全闭环锯片磨床数控系统开发

在锯片磨削过程中，由于机床自身运动误差和砂轮磨损，导致数控系统的指令磨削量与实际磨削量出现较大偏差(严重时实际磨削量几乎仅为指令磨削量的一半)，从而造成锯片厚度难以控制，生产率低等现象。一般的数控锯片磨床采用刀具半径固定补偿的方式，对磨削误差(主要是砂轮磨损量)进行补偿;但由于砂轮磨损量受磨削参数、锯片材质和砂轮材质等诸多因素的影响，因此，很难达到磨削误差精确补偿的目的，致使锯片磨削尺寸精度难以控制、生产率较低等问题至今无法得到根本解决。本文针对原数控锯片磨床的缺点与不足，探讨了在华中数控世纪星18i数控系统的基础上，通过增设锯片厚度实时在线自动测量功能，数控系统根据测量值与理论值的关系，确定磨削误差，并在磨削过程中进行误差实时补偿，从而实现对锯片磨削过程全闭环控制的方法。

1 全闭环锯片磨削的控制技术

1.1 全闭环锯片磨削的加工工艺

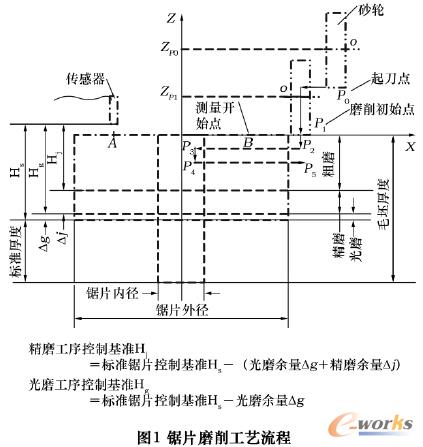
在实际加工中，锯片磨削分为粗磨、精磨和光磨三道磨削工序，用户可以通过人机界面，设置各工序的磨削余量、进给量和磨削速度等参数。全闭环锯片磨削工艺流程如图1所示，磨削前砂轮处于起刀点P0的位置;磨削加工开始，首先完成毛坯厚度的测量，判断是否满足正常磨削条件(即毛坯厚度应不超过规定公差范围)，若满足条件，则计算出砂轮在磨削初始点P1时其中心的坐标值ZP1，以及第一次进行磨削的砂轮理论进给量和磨削速度，反之，产生报警信息并退出加工。当毛坯测量完成，且满足正常磨削条件时，砂轮从起刀点P0快速运动到磨削初始点P1，开始磨削循环加工。一个磨削循环的路径为:Z轴进给→X轴由外向中心进给→Z轴进给→X轴由中心向外退出。每完成一个磨削循环，系统便对锯片厚度进行一次测量。根据锯片厚度的测量值，计算本次磨削循环产生的磨削误差，以磨削误差实时补偿原则，确定下一个磨削循环的加工参数，随后继续进行磨削循环加工;当锯片厚度测量值≤进入精磨的理论厚度或进入光磨的理论厚度时，分别进入精磨工序的磨削循环加工或光磨工序的磨削循环加工;当锯片厚度测量值与锯片标准厚度之差在允许的公差范围内时，整个磨削循环加工结束，砂轮快速返回到起刀点P0，磨削加工过程结束。对于同批量锯片的磨削加工，将新锯片毛坯安装好后，不作任何调整，只需按下循环启动键，则系统完成自动加工。

1.2 全闭环锯片磨削的控制策略

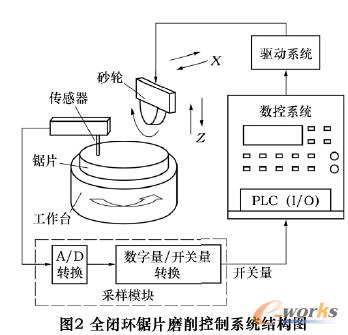
1.2.1 全闭环锯片磨削机床系统结构

全闭环锯片磨削机床系统是在华中数控世纪星18i数控锯片磨床基础上，通过增设基于电涡流位移传感器的测量系统而构成的，系统结构如图2所示。测量系统由量程为0～4mm的电涡流位移传感器和采样模块组成，实现对锯片表面与传感器测量头之间距离的在线测量。传感器输出的正比于距离值的电压信号，经采样模块首先转换为12位数字量(测量灵敏度约为:0.001mm/位)，再转换为数控系统PLC的I/O接口能识别的开关量信号。在每一次测量期间，数控系统的PLC以8ms的执行周期，对I/O接口的测量值进行150次采样。150个数据反馈到数控系统后，经滤波处理和数据转换，获得实际锯片厚度值。

1.2.2 全闭环锯片磨削的控制策略

全闭环锯片磨削系统对磨削加工过程的控制选择G代码程序控制方式。不过，由于在磨削加工过程中，磨削工序类型、加工参数和磨削工艺流程，均由锯片厚度的测量值实时决定，而标准的G代码程序不具备从数控系统外部I/O接口获取测量数据的能力，为此，必须对数控装置的系统软件进行相应的开发，创建一个软件磨削控制器。软件磨削控制器主要实现对来自数控系统外部I/O接口的测量数据的采样计算，并将计算信息实时传递给G代码程序，从而实现由锯片厚度测量值实时控制磨削加工过程的控制思想。由此可见，全闭环锯片磨削加工的控制策略是利用G代码程序和软件磨削控制器相互协调运行，共同完成对磨削加工过程的控制。本系统中，G代码程序与软件磨削控制器的执行采用并行运行方式，其控制的主要原理是:每当G代码程序执行到特定位置时，如图中砂轮由X轴从中心向外退回到与传感器测量头安装位置A点对称的B点位置时(图1)，由G代码程序激活软件磨削控制器，再由软件磨削控制器启动测量系统，对锯片厚度进行采样计算。磨削控制器根据本次测量值，进行一系列的判断，如毛坯是否满足正常磨削条件、磨削加工是否结束等;若加工尚未结束，则确定下一次磨削循环的磨削工序类型，并通过前后两次磨削循环后的测量值，确定本次磨削循环的实际磨削量Δ′Z，按式(1)计算出本次磨削循环的磨削误差δZ和砂轮的磨损量ΔR;并