基于小波变换的ECG信号压缩及其FPGA实现

。

通过对输入ECG信号的仿真分析以及信号在MATLAB中使用wavedec函数进行分解得到的结果与基于本设计的变换核的1D-DWT变换的仿真结果的比较(如图4)，可以了解本变换核的性能。由于采用了流水线操作原理以及采用了流水线架构的乘加逻辑，系统的变换速度得到了很大的提高。该变换核在输入3个数据后得到第一个低频变换系数，在输入5个数据后即开始得到第二个低频变换系数和第一个高频变换系数，之后每输入2个数据就各得到一个高频和低频分量。通过控制逻辑将这些分量在适当的时候输出并存储起来就可以完成本次小波变换。

逆变换的设计方法与正变换的方法相似，根据式(3)和式(4)，首先由输入的高通、低通滤波系数序列计算出偶序列，再根据偶序列的数值计算出奇数列的数值，对于边界问题也采用“补零”的方法。逆变换设计的方法是在图3中将变换输入单元改为变换后的序数，通过逐个将数据输入并经过依据式(3)和式(4)重新设置权重，即可实现该小波的反变换核。同时通过计算单元，利用偶序列的计算结果计算出奇序列的数值，最终实现原始信号的重建过程。

由于本设计旨在使用DWT变换实现对ECG信号的压缩，因此，采用了5级小波变换的措施以减小数据量，实现最大程度的低失真压缩，其原理图如图5所示。

该模块首先将ECG信号分成1 024点的帧，然后逐个送入5级小波变换模块。在该模块中的控制将选通输入信号为外部送入的ECG信号作为输入1D-DWT的变换对象，变换后的对象存储在C5、D5、D4、D3、D2、D1中。D1的大小为512 B，存放的是第一次变换后的高频分量，低频分量依次存储于C5D5D4D3D2。接着控制逻辑将选通低频分量C5D5D4D3D2作为1D-DWT的变换对象，变换后的高频分量存储于D2，低频分量存储于C5D5D4D3，即实现了对于ECG信号的2-level DWT变换。这样经过5次变换后得到的变换结果为C5：32 B、D5：32 B、D4：64 B、D3：128 B、D2：256 B、D1：512 B。通过设定阈值可以实现噪声可控的量化，并建立段数据的码书，以实现数据与编码之间的对应。对于ECG信号的重建，可以理解为小波分解压缩的逆过程。首先将压缩后的信号解码后按序送入C5D5D4D3D2D1，控制逻辑电路将逐层对信号进行反变换，从而得到重建后的信号。当阈值设置大于零时，重建的信号将会存在一些失真，即为有损压缩，若要实现无损压缩，则只需将阈值设为零即可，但压缩率会有所降低。

4 实验数据及结果

本设计的5级小波变换模块在quatus中采用EP2C35F672C6编译后占用的资源及性能情况如表1所示。

利用该模块分别对采集的不同ECG信号和经过放大和取整处理之后的MIT的ECG信号进行压缩实验，使用两个指标来衡量本压缩算法的性能。一个是压缩比CR(Compression ratio)，另一个是均方根误差PRD（percent root mean square difference）。具体的计算公式为：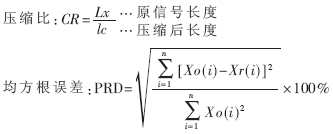

其中Xo(i)、Xr(i)分别代表原始心电信号数据和重建后的心电信号数据。得到的压缩率与阈值及信号的对应数据如表2所示。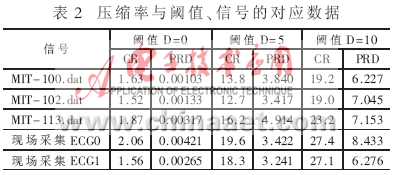

从表中可以看出，本算法能在一定的PRD范围内获得较大的压缩比，在阈值D等于零时，依靠码本编码算法依然获得了一定得压缩比，但由于小波变换核在运算过程中具有右移位操作，还是造成了很小的失真，即在D=0时仅能做到准无损压缩。图6为阈值等于5时，对MIT-100.dat信号重建的结果。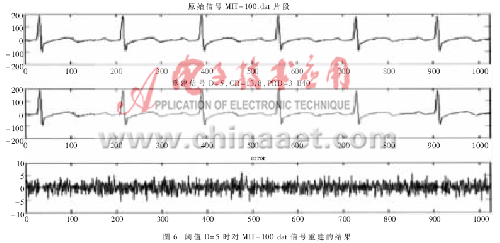

通过对5/3小波变换的研究，设计实现了5层小波变换及其反变换的FPGA硬件实现，并对结果进行了仿真及实例验证，得到了很好的效果。采用Altera的DSP Builder进行开发，具有使用灵活、开发周期短的特点。采用 FPGA实现小波变换与用 DSP处理器的方法相比，具有速度快、数据宽度可任意设置的特点，并且硬件语言具有可移植性的特点，具有更强的通用性。由于在现代信号处理中的大量应用，可以将小波变换核设计成可重用的IP。

在完成小波变换的FPGA实现后，本文将其应用于ECG信号的压缩，通过多层小波变换与编码的结合，实现了ECG信号实时有效的压缩和重建。