基于FPGA流水线分布式算法的FIR滤波器的实现

随着数字技术日益广泛的应用，以现场可编程门阵列（FPGA）为代表的ASIC器件得到了迅速普及和发展，器件集成度和速度都在高速增长。FPGA既具有门阵列的高逻辑密度和高可靠性，又具有可编程逻辑器件的用户可编程特性，可以减少系统设计和维护的风险，降低产品成本，缩短设计周期。

分布式算法是一种以实现乘加运算为目的的运算方法。它与传统算法实现乘加运算的不同在于执行部分积运算的先后顺序不同。简单地说，分布式算法在完成乘加功能时是通过将各输入数据每一对应位产生的部分积预先进行相加形成相应部分积，然后再对各部分积进行累加形成最终结果，而传统算法是等到所有乘积产生之后再进行相加来完成乘加运算的。与传统算法相比，分布式算法可极大地减少硬件电路规模，很容易实现流水线处理,提高电路的执行速度。

FPGA有着规整的内部逻辑块阵列和丰富的连线资源，特别适合细粒度和高并行度结构特点的数字信号处理任务，如FIR、FFT等。本文详细讨论利用FPGA实现FIR滤波器的设计过程，并且对设计中的关键技术——分布式算法进行详细描述。

1 FIR和分布式算法

1.1 FIR的基本概念

FIR滤波器的数学表达式为：

式中,N是FIR滤波器的抽头数；x(n)表示第n时刻的输入样本；h(i)是FIR滤波器的第i级抽头系数。

普通的直接型FIR滤波器结构如图1所示。

FIR滤波器实质上是一个分节的延迟线，把每一节的输出加权累加，便得到滤波器的输出。对于FIR滤波器，幅度上只需满足以下两个条件之一，就能构成线性相位FIR滤波器。

h(n)=h(N-1-n) (2)
h(n)=-h(N-1-n) (3)

式(2)称为第一类线性相位的幅度条件(偶对称)，式(3)称为第二类线性相位的幅度条件（奇对称）。

1.2 FIR滤波器的优化

在实际应用中，为了减少逻辑资源的占有量和提高系统的运行速度，对FIR滤波器需要进行优化处理。本文采用的优化主要有两种：一种是对表达式进行优化，另一种是在FPGA实现中利用特有的查找表进行优化。

1.2.1 表达式的直接优化

对于线性相位因果FIR滤波器，它的系数具有中心对称特性，即h(i)=±h(N-1-i)。令s(i)=x(i)±x(N-1-i)，对于偶对称，代入式(1)可得：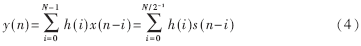

根据方程(4)，线性相位FIR滤波器的直接型结构可以改为如图2所示的结构，从而使N次乘法减少为[N/2]次，加法次数增加了[N/2]次（N为偶数），总的运算量减少。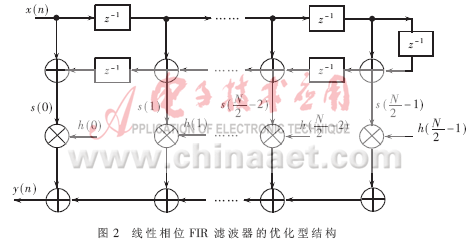


1.2.2 利用查找表进行设计优化

由于实现的是固定系数的FIR滤波器，所以可以利用简化的乘法器（如查找表）减少设计所耗用的器件资源。
以一个8阶FIR滤波器为例来说明在FPGA实现中优化的过程。假定滤波器的输入为2bit的正整数，由式(4)可以得到输出为：

y(n)=s(0)h(0)+s(1)h(1)+s(2)h(2)+s(3)h(3) （5）
这时的乘法和加法就可以并行地采用查找表实现，其结构示意图如图3所示。

在图3中，右面4个信号是输入的低位bit，左边是输入信号的高位bit。低位和P1最多使用4bit，由于系数固定，查找表实现起来很方便；高位和P2可按同样方法计算。在该结构中，部分积P1和P2可以利用Virtex-E的4输入查找表实现，所有的计算都可并行完成。由于输入为2bit，因此只用了一个加法器；对于更多位数的输入来说，将需要更多的加法器。这样就实现了将乘法器转化为加法器，减少了逻辑资源，优化了设计。

1.3 分布式算法

分布式算法在20多年前被首次提出，但直到Xilinx发明FPGA的查找表结构以后，分布式算法才在20世纪90年代初重新受到重视，并被有效地应用在FIR滤波器的设计中。下面介绍分布式算法的原理。

式(1)可以用下式表示：

式中，hi即h（i），xi(n)即x(n-i)，N为滤波器的抽头数。

把数据源数据格式规定为2的补码形式，则：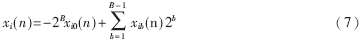

式中，xib(n)为二进制数，取值为0或1；xi 0(n)为符号位，为1表示数据为负，为0表示数据为正。将(7)式代入(6)式可得：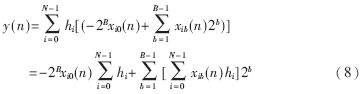

由此可以看出，方括号中是输入变量的一个数据位和所有滤波器抽头系数h0～hi的每一位进行“与”运算并求和。而指数部分则说明了求和结果的位权，整数乘以2b就是左移b位，对此可以通过硬件连线实现，不占用逻辑资源。这样就可以通过建立查找表来实现方括号中的运算，查找表可用所有输入变量的同一位进行寻址。

2 系统设计与实现

下面以一个16阶的线性相位FIR低通滤波器为例说明设计的过程。

2.1 设计指标及参数提取

2.1.1 滤波器的设计指标

采样频率：≥50MHz 归一化截止频率:0.4MHz
类 型：低通 输入数据宽度：8位
阶 数：16阶 输出数据宽度：16位

2.1.2 参数提取

采用汉宁窗函数(Hanning)设计16阶线性相位FIR数字滤波器，并提取其特性参数。

这里需要注意的是：下载到FPGA的程序是按照FIR滤波器的差分方程式编写的。由于从MATLAB中算出的系数h(n)的值是一组浮点数，而FPGA器件只进行定点值的计算，所以要进行浮点值到定点值的转换。假定“1”对应10000000000000000(17位，相当于乘上65536)。

用汉宁窗(Hanning)进行设计，此16阶FIR数字低通滤波器特性参数经过换算如下：
h[0]=h[15]=0000 h[1]=h[14]=0065 h[2]=h[13]=018F h[3]=h[12]=035A h[4]=h[11]=0579 h[5]=h[10]=078E h[6]=h[9]=0935 h[7]=h[8]=0A1F

2.2 系统具体实现步骤

2.2.1 查找表的建立

我们知道，如果滤波器抽头数N过多，用单个查找表就不能够执行全字（因为查找表位宽＝滤波器抽头数的数量）。在这种情况下，可以将表的地址输入位数（即滤波器抽头数N）进行降低，即利用部分表并将结果相加。如果加上流水线寄存器，这一改进并没有降低速度，但是却可以极大地减少设计规模，因为查找表的规模是随着地址空间，也就是滤波器抽头数N的增加而呈指数增加。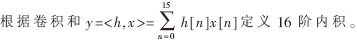

滤波器抽头数是16个，考虑到线性FIR滤波器的偶对称特性，只考虑8个独立滤波器抽头数，则需要一个28×8的表(其中指数8指的是8个滤波器抽头数，后面的8指的是输入数据的位宽)。但是Virtex-e FPGA只能提供4输入的查找表，所以要对查找表的地址进行电路分割。将8位地址线分为高4位和低4位，分别作为两个24×8的查找表的地址输入，从而指数倍地节省了硬件资源。

查找表的具体内容如表1所示。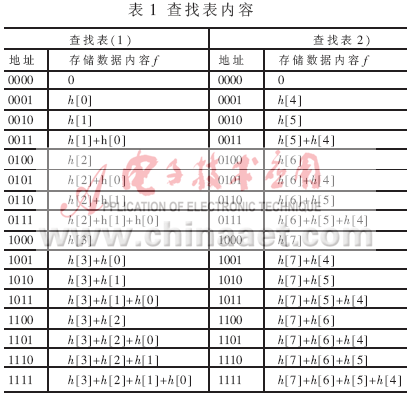


2.2.2 查表计算部分积累加和的过程

假定输入数据x[n]的值x[0]=110=000000012c,x[1]=-110=111111112c,x[2]=310=000000112c,x[3]=210=000000102c。(注：2c代表用二进制补码表示,最高位为符号位。)

查找表(1)的部分积如表2所示。

数据校验结果:h[0]x[0]+h[1]x[1]+h[2]x[2]+h[3]x[3]＝2812。
说明利用分布式查表算法的计算结果与直接计算结果相同，算法正确无误。
查找表(2)的查表计算结果依此类推。只是需要注意：查找表(2)的数据输入x是8位数据x[4]、x[5]、x[6]、x[7],而不是x[3]、x[2]、x[1]、x[0]。根据系数偶对称性质，x[8]、x[9]、x[10]、x[11]查查找表(2)，x[12]、x[13]、x[14]、x[15]查查找表(1)。