有射频基础后让你秒懂“史密斯圆图”的真谛

不管多么经典的射频教程，为什么都做成黑白的呢？让想理解史密斯原图的同学一脸懵逼。

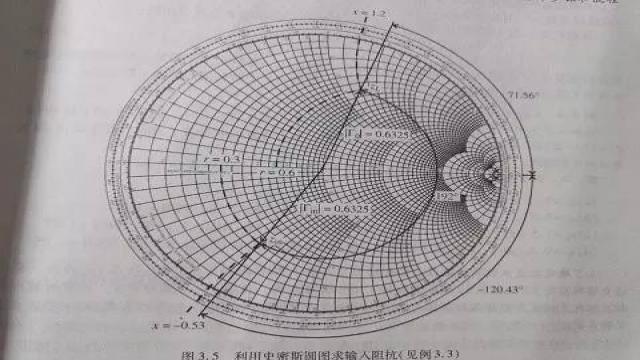
这是什么东东？

今天解答三个问题：

1、是什么？

2、为什么？

3、干什么？

1、是什么？

该图表是由菲利普·史密斯(Phillip Smith)于1939年发明的，当时他在美国的RCA公司工作。史密斯曾说过，"在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣"。

史密斯图表的基本在于以下的算式。

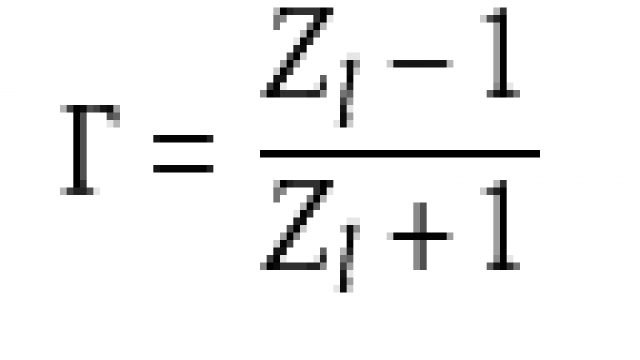
当中的Γ代表其线路的反射系数(reflection coefficient)

即S参数（S-parameter）里的S11，ZL是归一负载值，即ZL / Z0。当中，ZL是线路本身的负载值，Z0是传输线的特征阻抗（本征阻抗）值，通常会使用50Ω。

简单的说：就是类似于数学用表一样，通过查找，知道反射系数的数值。

2、为什么？

我们现在也不知道，史密斯先生是怎么想到"史密斯圆图"表示方法的灵感，是怎么来的。

很多同学看史密斯原图，屎记硬背，不得要领，其实没有揣摩，史密斯老先生的创作意图。

我个人揣测：是不是受到黎曼几何的启发，把一个平面的坐标系，给"掰弯"了。

世界地图，其实是一个用平面表示球体的过程，这个过程是一个"掰直"。

史密斯原图，巧妙之处，在于用一个圆形表示一个无穷大的平面。

2.1、首先，我们先理解"无穷大"的平面。

首先的首先，我们复习一下理想的电阻、电容、电感的阻抗。

在 具有电阻、电感和电容的电路里，对电路中的电流所起的阻碍作用叫做阻抗。阻抗常用Z表示，是一个复数，实际称为电阻，虚称为电抗，其中电容在电路中对交流 电所起的阻碍作用称为容抗 ,电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍作用总称为电抗。 阻抗的单位是欧姆。

R，电阻：在同一电路中，通过某一导体的电流跟这段导体两端的电压成正比，跟这段导体的电阻成反比,这就是欧姆定律。

（理想的电阻就是 实数，不涉及复数的概念）。

如果引入数学中复数的概念，就可以将电阻、电感、电容用相同的形式复阻抗来表示。既：电阻仍然是实数R（复阻抗的实部），电容、电感用虚数表示，分别为：

说明：负载是电阻、电感的感抗、电容的容抗三种类型的复物，复合后统称"阻抗"，写成数学公式即是：阻抗Z= R+i(ωL–1/（ωC）)。其中R为电阻，ωL为感抗，1/（ωC）为容抗。

（1）如果(ωL–1/ωC) > 0，称为"感性负载"；

（2）反之，如果(ωL–1/ωC) <>

我们仔细看阻抗公式，它不再是一个实数。它因为电容、电感的存在，它变成了一个复数。

电路中如果只有电阻，只影响幅度变化。

我们通过上图，我们知道，正弦波的幅度发生了变化，同时，相位也发生了变化，同时频率特性也会变化。所以我们在计算的过程中，即需要考虑实部，也需要考虑虚部。

我们可以在一个复平面里面，以实部为x轴、以虚部为y轴，表示任意一个复数。我们的阻抗，不管多少电阻、电容、电感串联、并联，之后，都可以表示在一个复平面里面。

在 RLC 串联电路中，交流电源电压 U = 220 V，频率 f = 50 Hz，R = 30 Ω，L =445 mH，C =32 mF。

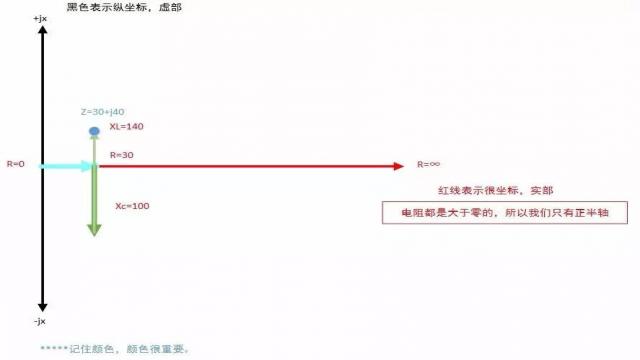
在上图中，我们看到通过几个矢量的叠加，最终阻抗在复平面中，落在了蓝色的圆点位置。

所以，任意一个阻抗的计算结果，我们都可以放在这个复平面的对应位置。

各种阻抗的情况，组成了这个无穷大的平面。

2.2、反射公式

信 号沿传输线向前传播时，每时每刻都会感受到一个瞬态阻抗，这个阻抗可能是传输线本身的，也可能是中途或末端其他元件的。对于信号来说，它不会区分到底是什 么，信号所感受到的只有阻抗。如果信号感受到的阻抗是恒定的，那么他就会正常向前传播，只要感受到的阻抗发生变化，不论是什么引起的（可能是中途遇到的电 阻，电容，电感，过孔，PCB转角，接插件），信号都会发生反射。

钱塘江大潮，就是河道的宽度变化引起了反射，这跟电路中阻抗不连续，导致信号反射，可以类比。反射聚集的能量叠加在一起，引起的过冲。也许这个比喻不恰当，但是挺形象。

那么有多少被反射回传输线的起点？衡量信号反射量的重要指标是反射系数，表示反射电压和原传输信号电压的比值。

反射系数定义为：

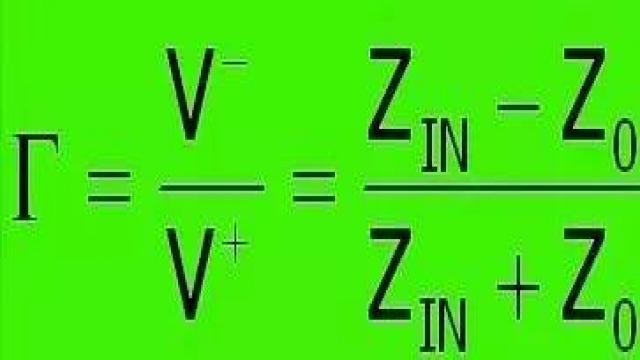
其中：Z0为变化前的阻抗，ZIN为变化后的阻抗。假设PCB线条的特性阻抗为50欧姆，传输过程中遇到一个10