基于WLS-KF的GPS非线性动态滤波研究

摘要：为了提高动态定位精度，将卡尔曼(KF)算法应用到GPS非线性动态定位解算中，提出加权最小二乘一卡尔曼滤波(WLS-KF)算法。通过加权最小二乘(WLS)算法得到近似的线性化模型，再将KF算法应用到这个线性化模型进行校正。因此既保持了KF算法能够对系统状态进行最优估算的优点，同时对各个测量值进行了联系制约，具有更高的精度。结果表明，这种方法精度介于EKF和UKF之间，且实现容易，预测可靠，具有实际应用价值。
关键词：全球定位系统；卡尔曼滤波；加权最小二乘；非线性

0 引言
卡尔曼滤波(KF)是一个不断预测、修正的递推过程，已经越来越多地应用于动态数据处理中。然而在KF模型中，要求观测方程是线性形式、状态噪声和测量噪声是白噪声。为了解决这种矛盾，将KF理论应用到非线性领域中，扩展卡尔曼滤波(EKF)应用而生，它围绕状态估计值对非线性系统进行一阶Taylor展开使其线性化，但它存在如下不足：一是当非线性函数Taylor展开式的高阶项无法忽略时，会产生较大的线性化误差；二是EKF假定噪声均为正态白噪声，但是一个正态自噪声经过非线性变换后通常不再呈现正态性；三是只有在雅可比矩阵存在时才能线性化，而很多应用中雅可比矩阵很难求。针对这种情况，Julier和Uhlmann等人提出了一种基于非线性变换——Un-scented变换(UT)的卡尔曼滤波算法(UKF)。它通过确定性采样得到的一组sigma点，可以获得更多的观测假设，对系统状态的均值和协方差的估计更为准确，同时由于该算法采用了非线性的状态方程和观测方程，从而避免了线性化误差。目前，EKF和UKF算法被广泛应用于GPS非线性动态滤波研究中，并取得良好的定位效果。
本文给出了一种加权最小二乘一卡尔曼滤波(WLS-KF)算法，它利用一组离散采样点，通过WLS方法产生近似线性化预测模型，然后用KF算法对此模型进行校正。以该算法为思路，将其应用在GPS非线性动态滤波定位解算中，仿真结果表明该算法精度介于EKF和UKF之间，从而实现了对目标较高精度的定位和跟踪。

1 算法描述
1．1 WLS算法
LS算法是现代测量技术中数据处理的基本工具，这种方法的特点是算法简单，在估计解算时，不需要知道与被估计量以及观测量有关的任何统计信息。
设X为待估参数矢量，观测矢量为L。观测方程为：

式中：v为观测误差。用泰勒定理展开，得到线性化的观测方程为：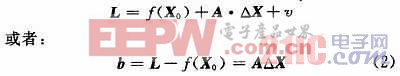

式中：A是系数矩阵；f(X0)表示用先验参数计算的理论观测向量；b表示拟合后的残差；△X是对先验参数的小修正向量。
LS算法的指标是使各次观测量与由参数估计得到的观测量之差的平方和最小，即：

要使上式达到最小，当对观测矢量的质量有所了解时，设置各个测量值的权重，得到WLS算法的解为：

若更新后的Xk尚未达到求解精度，则Xk可作为第k+1次迭代的起始点，继续进行上述运算。
1．2 KF算法
KF算法对一个离散时间线性系统的状态进行最优估计，使系统状态的估计值有最小均方误差(MMSE)。
考虑一个多输入多输出的离散时间线性动态系统，其状态方程可表示为：

向量wk和vk分别表示状态噪声和测量噪声，假设它们都是均值为零的正态白噪声且相互独立，即：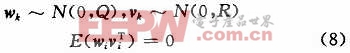

KF算法通过如下的时间更新过程和测量更新过程来对系统状态进行估计。

计算完测量更新方程后，整个过程再次重复，上一次计算得到的后验估计被作为下一次计算的先验估计。
1．3 WLS-KF算法
1．3．1 基本思想
算法基本思想是通过WLS方法计算随机变量经过非线性变换后的分布参数，它利用离散个加权点来确定近似直线。
设待确定的近似线性化模型为：

式中：(xn，f(xn))表示设置的离散加权点；p(xn)表示其对应的权系数，n=1，2，…，n。
1．3．2 算法流程
将加权最小二乘线性化方法同KF算法相结合，便得到了WLS-KF算法。具体的算法流程如下：
(1)设置矩阵A，b和加权矩阵W；
(2)将A，b和W带入式(17)，求出线性化系数矩阵A1，常数向量b1；


2 实验结果与分析
基于运动载体为质点的假设建立目标运动模型，考虑一个二维平面曲线运动系统，状态定义为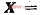，分别表示二维方向上的位置变量、速度变量、载体相对于起始位置的转弯角度及接收机钟差。

式中：wk，vk和εk为相互独立的高斯白噪声序列，wk～N(0，10)，vk～N(0，10)，εk～N(0，1)。此系统是具有可加噪声的离散非线性时变系统，观测时间为100 s，观测周期为1 s。WLS-KF和EKF，UKF算法的二维预测结果分别如图1，图2所示，预测结果误差分析见表1。

为便于比较，算法中使用的随机数据均来自于提前保存好的随机序列。结果表明，WLS-KF算法的计算量适中，精度介于EKF和UKF之间，且效