利用超声散射测量材料内部微裂纹分形参数的新方法

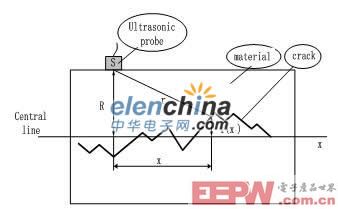
图-1 分形微裂纹几何示意图

事实上，测试中用到的超声波往往是脉冲波，所以，在研究中采用连续波被高斯函数调制的形式，有以下的表达式：
(4)
式中，g(t)是零均值的高斯函数，可表示如下：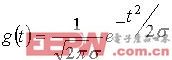
(5)
实测中，把超声传感器S当作一个点源，向外发射球面脉冲波。当点源S与裂纹间的距离r 远大于超声传感器的晶片直径d (r>>d)时，裂纹上一点在时刻 t 接收到的超声波为：
(6)
式中， c 超声波的传播速度。

当超声波到达裂纹表面时，在裂纹表面产生散射。目前还没有确切地算法可用来计算超声波的散射回波声场。在研究中，我们把它当作二次点源，向外辐射球面波。我们将利用基尔霍夫近似来计算由裂纹散射的超声回波。此时，超声回波可看作由裂纹表面上的二次点源辐射的球面波的合成，并假设超出超声波照射范围的裂纹上的点没有声波的散射，散射回波是关于超声传感器所在的位置的中心线对称的，在计算超声回波时，忽略裂纹上的多次散射回波，不计裂纹上没有被直接照射的点的超声回波，并且认为裂纹都是近轴分布的，我们可以得到下面的超声回波的表达式：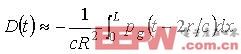
(7)
式中， 是超声传感器与裂纹上点的距离。
是超声传感器到裂纹中心线的垂直距离。
是超声传感器中心线到超声最大照射范围的单边长度。

从图-1所示的几何关系可以得到：
(8)
用方程式(8)中的 替代超声回波计算式中的 ，可以将超声回波化为：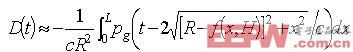
(9)
特别地，我们可以取某一时刻 的超声回波作为研究对象，时刻 可以选为 ，即超声波从传感器中心线返回时刻。则在这一时刻的超声回波可以表示为：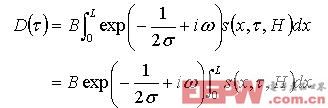
(10)
式中,

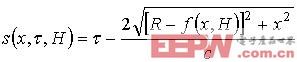
方程 (10) 就是关于超声散射回波与微裂纹分形参数（ Hurst指数）的关系模型。当方程中除Hurst指数外的其它参数给定时，我们就可以根据试验测得的时刻τ的裂纹散射回波D(τ)来确定裂纹的分形参数H。 我们可以利用这个关系来实现微裂纹分形参数的测量。

考虑到方程(10)中积分项不能直接计算，因为f(x,H) 没有导数，所以我们采用数值计算的方法来近似计算这一积分，在这种情况下，方程(10)可化为：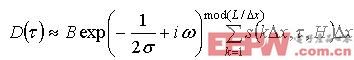
（11）
如果步长 Δx 选的足够小，计算结果可以保证精度的要求。

4 模型数值仿真与分析

作为模型的实际应用，我们分别计算了模型在不同分形参数、不同的测量距离和不同材料上的超声散射回波。

试验中，采用了三种不同的材料，分别是铝、钢和和玻璃，超声波在三种材料中的声速分别为6300m/s，5900m/s 和5570m/s。超声波的中心频率为5MHz，超声传感器的晶片直径为10mm。

图-2是不同分形参数的微裂纹在时刻 时的超声散射回波，图中分别给出了三种材料对应的仿真结果。从图中可以看出，不同分形参数的裂纹对应不同的超声散射回波，表明在时刻 的超声散射回波可以表征裂纹的不规则程度和复杂性，并且超声散射回波与裂纹的 Hurst指数是一一对应的，所以，我们可以用这种方法来测量微裂纹的分形参数。

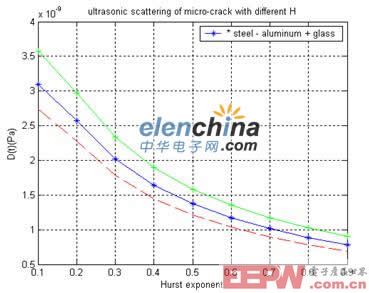
图-2 不同分形参数微裂纹在时刻 的超声散射回波

图-3是在不同的测量距离时，三种不同材料内部微裂纹的超声散射回波。图中分别给出了Hurst指数为0.2和0.8两种情况下，三种不同材料的超声散射回波的仿真结果。从图中可以看出，当测量距离增加时，超声回波快速下降，这与实际情况是相符的。同时可以看出，当测量距离一定时，超声回波与Hurst指数是一一对应的。仿真结果表明，我们所建立的测量模型是正确可行的。所以，可以采用这种方法，在不需要对裂纹进行剖切的情况下，对不同材料内部的微裂纹的分形参数进行测量，该方法与传统的测量方法相比，更加方便。

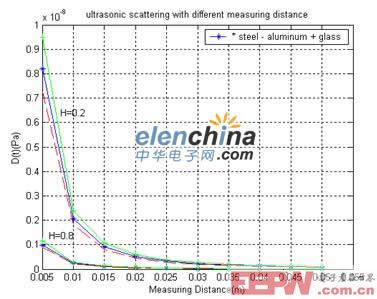
图-3 不同测量距离时材料内部微裂纹的超声散射回波

5 结论

论文提出了一种利用超声波对材料内部微裂纹分形参数（Hurst指数）进行测量的新方法。论文首先采用一维分形布朗运动（FBM）来描述材料内部的微裂纹，然后，建立了微裂纹超声散射回波的数学模型，该模型建立起了时刻 的超声回波信号与裂纹分形参数之间的关系，从理论上说明了这种测量方法的可行性。最后，对不同分形参数、不同材料和不同测量距离的情况分别进行了数值仿真，试验结果也表明了这种方法的可行性。与传统的裂纹分形参数测量方法相比，该方法具有高效和省时的特点。