基于支持向量机的无人机视觉障碍检测

摘要：自主障碍检测与回避是无人机低高度飞行时保障其生存性的一项关键技术，有重要的研究意义。通过对机器视觉原理的研究，考虑到支持向量机方法能同时减小匹配难度和计算量，实时性能、泛化性能良好，故采用该方法通过离线监督学习，将无人机前视图像分割为天空与非天空2部分，并将非天空部分作为需要回避的障碍，实现无人机基于视觉的障碍检测系统，为后续的视觉制导提供信息。实验结果表明，支持向量机能有效准确地实现图像的天空分割，并具有良好的泛化性能。
关键词：低高度飞行；支持向量机；图像分割；障碍检测

0 引言
美国军方将地形跟随飞行分为3类低空飞行模式(Low AltitLlde)：低高度飞行(Low Level)、轮廓线飞行(Contour)、贴地飞行(Nap of the Earth)。以上三种低空飞行模式都提供了最低的飞行高度和最大程度的隐蔽性。低高度飞行的主要障碍是环境中的地形、植被和人工建筑，它通过在障碍上方飞行回避了障碍，并实现最低的飞行高度，因此对障碍物的检测成为低高度飞行中的重点问题。
SVM方法是建立在统计学习理论的VC维理论和结构风险最小化原理的基础上。根据有限样本信息在模型的复杂性和学习能力之间寻求最佳折衷，以期获得最好的泛化能力，它是一种小样本的机器学习方法，在减小匹配难度的同时也大大减小了计算量，可以满足实时性要求。因此本文研究利用这种方法，将无人机前视图像分割为天空与非天空2部分，并将非天空部分作为需要回避的障碍。

1 支持向量机基本理论
支持向量机是基于分离超平面的。对任何一套线性可分的数据，存在值ω和b使数据集中的任意数据点x可以用下列公式分割：
y(ω·x)+b>0 (1)
式中：y=1取决于数据点属于2个种类中哪一类(正类为+1，负类为-1)，当处理一个有限数据集时，式(1)可以表述为：

式中：xi是训练集中的训练点；x是待分类的测试点；αi为权重系数；yi为类别。
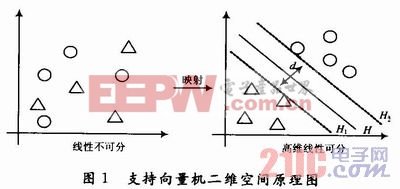
当数据集线性不可分时，通过内积核函数φexample(z)=(z，z2)将数据集非线性地映射到高维特征空间，变为线性可分的数据集，然后在高维特征空间建立一个不但能将2类正确分开，而且使分类间隔最大的最优分类面。图1是支持向量机思想在二维空间中的原理图。其中，H为最优分类面；H1，H2分别为过各类样本中离分类线最近的、且平行于分类线的直线；H1，H2之间的距离叫作分类间隔d。

在高维特征空间中，式(2)变为：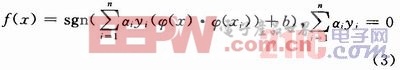

如果有一种方式可以在特征空间中直接计算(φ(x)·φ(xi))，就像在原始输入点函数中一样，就有可能将2个步骤融合到一起建立一个非线性的学习器，这样直接计算的方法称为核函数法。核函数定义为：
K(x，xi)=φ(x)·φ(xi) (4)
这样可以得到SVM分割函数的最终形式：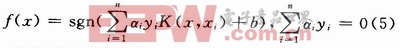

采用不同的核函数，SVM算法可以构造不同的学习机。这一特点提供了解决算法可能导致“维数灾难”问题的方法，即在构造判别函数时，不是先对输入空间样本作非线性变换，再在特征空间中求解，而是先在输入空间比较向量(例如，求点积或是某种距离)，再对结果进行非线性变换。这样，大的工作量就可以在输入空间中完成，而不需要在高维特征空间中进行。常用的核函数有以下几种：


2 支持向量机的障碍检测算法实现
图像分割的核心就是要从整幅图像中划分出感兴趣的目标区域，所以图像分割可以看成是一个分类问题，考虑用支持向量机方法来解决图像分割问题。将分割问题转化为分类问题是本文算法的特点，本文利用支持向量机将无人机飞行试验时机载摄像机拍摄到的图像帧分为天空和非天空两部分，图2为支持向量机训练点采集图，图3是从无人机机载摄像机拍摄的视频流中提取的一帧图像。

(1)通过观察，在图2中随机选择30个天空像素点作为正类训练点，同样选择30个非天空像素点作为负类训练点。
(2)选择输入空间的特征向量，考虑到每一个像素点既有颜色特征(即它的RGB值)，也有它的空间特征(即它处于空间中的位置，或者说它周围像素点信息)，因此选择当前像素点的R，G，B和以当前像素点为中心的3×3方阵的平均Ave R，Ave G，Ave B这6个特征分量。
(3)利用标记好的样本对SVM进行训练，本文选择C-支持向量分类机，核函数选择高斯径向核函数，即K(x，xi)=exp{-|x-xi|2／σ2}，并通过试验法选择核函数参数。
(4)利用训练好的支持向量机对图3进行分割，得到分割效果图。
(5)对分割效果图进行形态学操作。

3 实验结果
不同样本分布对应不同的SVM模型，因为样本线性不可分，因此选择C-SVM进行训练。核函数参数的选择也会影响分割效果，不同参数情况下图像分割结果如图4所示。从上述这些图可以看出，σ的取值直接影响图像分割的效果，在一定的范围内，σ取值越小，分割效果越好，如果σ过小，会使分割效果变坏，如图5所示。然而当训练集线性不可分时，分类超平面存在错分，惩罚因子c控制对错分样本的惩罚程度，c越大，对错分的惩罚越重，它在最优超平面与最近的训练样本之间的距离最大，与错分样本数最少之间进行折衷，直接影响着分类器的容量，从而影响着分类器的泛化性能。随着c的增大，对错分样本的惩罚增大，错分样本减少，分类间隔减小，分类器的VC维增大，分类器的泛化性能变差；随着c的减小，对错分样本的惩罚减小，错分样本增多，分类间隔增大，分类器的VC维减小，分类器的泛化性能也变差。因此，c的取值不宜太大，也不宜太小。当c=1，σ=0．000 5时，分割效果较为理想，非天空区域中的黑色部分原图中白色墙壁反光造成的，如图7所示。