GPS软件接收机关键技术研究及实现

摘要：研究了CPS软件接收机的关键技术和具体实现。设计并实现了一种基于FFT的码相位并行的快速信号捕获方案；介绍了码跟踪环与载波跟踪环的算法流程并详细推导了伪距及精密伪距的计算过程，在建立载体运动模型的基础上运用卡尔曼滤波对定位结果滤波处理，提高了定位精度，减小了定位方差。通过实验，验证了文中软件接收机算法的可行性，接收机定位精度较高，定位均方差较小。
关键词：GPS；捕获；跟踪；伪距；卡尔曼滤波

GPS软件接收机(Software Receiver，SR)和硬件接收机比较，所完成的功能相同，都能进行定位、测速等，但实现的环境不同，SR是在PC机上完成，以软件的方式实现，这种软件方式非常灵活，它能处理各种类型的硬件采集的数据。在不改变硬件的情况下就很容易验证新的算法，这对研究强干扰信号、高动态跟踪等问题有很大意义，有利于节省开发成本，加快算法推进。
GPS软件接收机主要由基带信号处理和导航定位解算2个模块构成，基带信号处理包含信号捕获、跟踪，导航定位解算模块包含星历计算、伪距计算、定位解算。其中，信号的快速捕获、高动态信号的跟踪、高精度的定位等i部分是接收机中的关键技术。
文中以SR算法流程为主线，对接收机中的关键技术分别进行了研究：在信号的快速捕获方面，设计了一种新的捕获方案，使得捕获速度快而且结果准确；在高动态信号的跟踪方面，载波跟踪用三阶锁相环，码环采用二阶环，采用载波环辅助码跟踪环的方式，因而可以减小码环带宽，提高跟踪精度；在高精度定位方面，详细推导了伪距的计算，同时考虑精密伪距的影响，提高伪距测量精度；鉴于最小二乘法定位解算没有考虑载体运动模型这种缺点，本文运用卡尔曼滤波埘定位结果进行处理，以获得高精度的结果，而且有效地减小了定位方差。

1 SR构成模块
SR处理下变频之后的中频数字信号，对信号进行捕获、跟踪及数据解调等操作以实现GPS接收机的定位、授时、测速等功能。如图1所示，软件接收机处理的主要是下半部分。

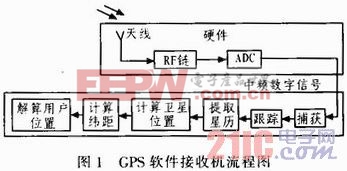
2 基带数字信号处理
基带数字信号处理由信号捕获和跟踪两部分构成，信号的捕获是接收机实现定位、测速等功能的第一步，用来确定接收到的信号中包含哪些颗卫星的信号，C／A码的起始点和多普勒频移，为跟踪作必要的准备。信号跟踪是对捕获到的卫星信号进行多普勒频移和C／A码相位的精准跟踪，是计算卫星星历、伪距等的前提。
由文献可知，由于接收机和卫星的相对运动，地面上静止的载体产生的多普勒频移在-5～5 kHz之间，对于高速运动的载体如导弹，产生的多普勒频移在-10～10 kHz之间。通常，对于一般的运动载体，多普勒频移搜索范围设在-7～7 kHz比较合理，捕获时多普勒频移搜索步长1 kHz，采用1 ms的数据。
文中采用基于FFT的并行码相位快速捕获方法，即在某一本地振荡频率下，能够同时计算出所有码相位的相关值，根据判决方式及门限确定卫星信号的多普勒频移及C／A码相位。此算法首先通过傅里叶变换由时域变换到频域，使时域中的相关运算转为频域中的乘法运算，然后通过傅里叶逆变换求时域内的各个码相位的相关值，其基本原理如下：
长度为N的有限序列x(n)的离散傅里叶变换是：

信号的捕获由粗捕获和精细捕获构成，粗捕获用来确定信号中是否含有某颗卫星信号、所含信号的C／A码相位起始点及分辨率为500 Hz(捕获步长1 kHz)的多普勒频移，精细捕获用来计算更精确的多普勒频移以满足跟踪环的要求。下面分别介绍文中设计的粗捕获和精细捕获实现方法。
2．1 粗捕获实现方法
在信号的多普勒频移处，会出现一个较大的相关峰值，在其他多普勒处，相关峰值逐渐变小直至大小类似噪声的相关值。
因此，在捕获时，以1 kHz的步长搜索多普勒频移，如果在某个多普勒频移下，当前相关峰值和之前已计算的较小的相关峰值比较，如果比值大于门限(通常取1．8左右)，则数据中存在该颗卫星的信号，至此可以确定分辨率为500 Hz的载波频率和码相位。否则，如果信号中不存在该颗卫星信号，可知在所有的多普勒搜索范围内，峰值比较平。
文中设计的这种粗捕获算法只需要计算各个多普勒频移下的相关峰值，无需计算相关均值或者次最大值，相对别的算法运算量小，实现速度快。
2．2 精细载波频率实现方法
粗捕获可以获得分辨率为500 Hz的载波，这不能满足载波跟踪环的要求，因此须通过精细捕获使本地振荡器频率和信号载波频率相差在几十赫兹内。
文中利用粗捕获得到的C／A码相位，缩短多普勒频移搜索步长计算相关值，采用二次曲线拟合的方法计算精细载频。
算法实现步骤如下：
1)利用粗捕获获得的C／A码起始位，产生1 ms本地C／A码序列，使之与中频信号相乘，剥离1 ms的C／A码，则输入信号变为连续载波信号。
2)粗捕获计算得到的多普勒频移是则可知信号多普勒频移在[fdop-500，fdop+500]Hz之内，以步长△fdop=250 Hz在fdop前后750 Hz范围内，与连续载波进行相关运算，得到7个相关值，取最大相关值及其两边的相关值，并取它们对应的多普勒频移。建立二次曲线的模型方程：

此时的X就是计算得到的精细多普勒频移，即是送入跟踪环路的多普勒频移。
这种精细捕获算法，运算量小，捕获结果准确，易于操作，而且对导航数据位的跳变不敏感。
2．3 完整捕获方案
根据载体和卫星的运动特点可知，地面上运动的载体，信号的多普勒频移分布±2，±3 kHz在的可能性比较大，因此先搜索这些多普勒频移，即在捕获时使用跳频搜索的方式，能够降低运算量，提高捕获速度。稳重采用的多普勒搜索的次序是[-2，2，-3，3，-1，1，-4，4，0，-5，5，-6，6，-7，7]，单位是kHz。
将上述的粗捕获算法、精细捕获算法和多普勒频移跳序搜索方法组合成一个完整的捕获方案。利用实际采集得到及信号模拟器产生的多组信号进行仿真验证，捕获费时约9 s，多普勒频移及C／A码相位捕获精度较高，能够满足跟踪环路要求。

3 卡尔曼滤波处理定位结果
传统定位解算方法仅利用了单点测量信息，未考虑载体的运动特性，定位精度易受观测噪声的影响。本文对载体的运动建模，采用卡尔曼滤波进行数据处理以得到高精度的定位结果。
根据载体运动的位置sk、速度vk、加速度ak之间的关系，建立载体运动方程为：


4 实验验证
为了验证所开发软件接收机算法的性能，分别进行了静态实验和动态实验。在实验中，利用东方联星公司研发的NewStar2100(以下简称NS)GPS中频数字信号采集器采集中频数字信号，在开发的软件接收机上进行定位解算；同时用NovAtel公司的FlexPax-G2L型高精度硬件接收机(以下简称G2L)的输出作为定位参考，其单点定位精度小于1．8m。
实验中的载波环采用三阶锁相环，码环采用二阶环，载波跟踪环噪声宽带为18 Hz，码跟踪环噪声宽带1 Hz，载波环辅助码环。定位解算后进行卡尔曼滤波时，系统噪声均方差取0．3 m／s3，ECEF坐标系下X，Y，Z方向上的观测噪声均方差分别是(8，8，14)m。
下面的实验分为两组，一组是静态定位结果比较，另一组动态定位结果比较。
4．1 静态定位结果比较
静态实验地点选在地点A。在该点采用G2L定位，并对观测时间段内的在ECEF坐标系下的定位结果取均值可得A1(-2171467．178，4386 130．452，4076269．089)m；对SR处理中频数字信号所得的ECEF坐标系下的定位结果取均值可得A2(-2171467．381，4386129．881，40762 69．242)m；二者的定位偏差(A2-A1)为(0．203，-0．571，0．153)m。
以上定位结果显示，SR与G2L的定位结果很接近，位置误差小。SR定位结果的输出频率为10 Hz，连续观测约36 s，以A1为原点，建立当地水平坐标系ENU，计算SR输出的瞬时定位结果相对于A1的位置误差。实际采集得到的信号中有8颗卫星的信号，这8颗星与接收机构成的GDOP值为3．9、19．6的两组定位结果。
位置误差均方差列在表1中，表中的E1，E2分别是卡尔曼滤波前、滤波后的位置误差均方差。