基于人工神经网络的过闸流量软测量研究

摘要：由于过闸流量与其影响因素(上游水位、闸门开度等)存在着复杂的非线性关系，给水流量的精确测量带来了困难。本文利用人工神经网络优良的非线性映射能力，建立了一个基于BP网络过闸流量软测量模型，并运用MATLAB神经网络工具箱以及碧口水电站实际数据对网络进行训练与验证。验证结果符合水流量测量精度的要求，为过闸流量的测量提供了一种简单，可靠的新方法。

引言

通过闸门的水流量是一个非常重要的参数。只有获得准确的流量值，才能实现对水资源的优化配置。目前对于过闸水流量的测量已形成了几种方法：流速仪法、水力学公式法以及曲线法^[1,2]。其中，被广泛运用与现场测流中的方法是流速仪法，它也是流量测量中最重要的方法。流速仪法是通过实测断面上的流速和水道断面积来确定流量的方法。测量时先在断面上布设测速垂线和测速点，再将流速仪放到测速点处测速，用分割法计算断面面积，推算出流量。虽然这种测流方法是目前的主导方法，但却存在着一些天生的缺陷：一是很难确定合适的测速垂线及测点，这是由于河道断面形状的不规则以及流速场分布情况复杂等原因造成的;二是实时性不高，测量时间比较长，从而导致管理部门不能及时了解过闸流量，耽误启闭闸门的最佳时机;三是需要的硬件资源比较多，因此大大增加了测流成本。鉴于此，研究一种新型的即简单、操作方便实时性又高，并且精度满足要求的测流方法已成为目前的迫切需求。而本文采用的BP网络软测量技术正好解决了以上诸多问题。

　　BP神经网络软测量模型

软测量技术是依据工业生产过程中有关的过程变量间的关联，通过一些能够检测的过程变量和相应的数学模型，来估计过程中用仪表较难检测的另一个变量的技术^[3,4]。通常而言，上游水位与闸门开度是比较容易测量的，而过闸流量却是一个非常难测量的变量。而对于一个固定的闸门，其过闸流量与上游水位及闸门开启高度有必然的联系，所以，以上游水位以及闸门的开启高度这两个值作为参数建立一个BP网络数学模型，可间接获得流量值。从而使得过闸流量的软测量得以实现。BP模型是一种多层感知机构，是由输入层、中间层(隐层)和输出层构成的前馈网络。因此，需要确定BP网络模型的层数及其各层的节点数。

网络层数的确定

理论上已证明：具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理函数。这就给我们提供了一个基本的设计BP网络的原则。增加层数主要可以更进一步降低误差，提高精度，但同时也使网络复杂化，从而增加了网络权值的训练时间，并可能陷入局部极小。而误差精度的提高实际上也可以通过增加隐含层中的神经元数目来获得，其训练效果也比增加层数更容易观察和调整^[5]。一般而言，BP网络模型中隐含层的层数为一层，这样网络既不会太复杂又不会陷入局部极小。因此，这里的BP网络采用两层结构，一层隐含层，一层输出层。各层之间实行全连接，层内神经元之间无连接。输出层神经元的激励函数为线性函数，隐层神经元的激励函数为S型(sigmoid)函数^[6]，即：

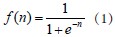
隐含层神经元数的确定

隐含层神经元数的选择在理论上并没有一个明确的规定。因此，选择合适的神经元数就显得十分麻烦。如果神经元太少，则网络不能很好地学习，需要的训练次数也多，训练的精度也不高。反而言之，如果隐含层神经元数选的太多，虽然功能会越大，但是循环次数也就是训练时间也会随之增加。另外可能还会出现其他的问题，如导致不协调的拟合。一般的选择原则是：在能够解决问题的前提下，再加上一到两个神经元以加快误差的下降速度即可^[7]。

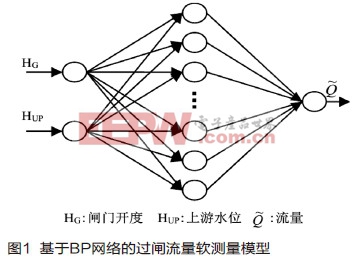
这里，我们通过对不同神经元数进行训练对比，以及通过简单的交叉验证法确定隐含层的神经元数为15个。基于BP网络的过闸流量软测量模型如图1所示。

模型的训练

BP网络学习规则

BP网络的学习过程分为两个阶段：

第一个阶段是输入已知学习样本，通过设置的网络结构和前一次迭代的权值和阈值，从网络的第一层向后计算各神经元的输出。

第二个阶段是对权和阈值进行修改，从最后一层向前计算各权值和阈值对总误差的影响，据此对各权值和阈值进行修改。

以上两个过程反复交替，直到达到收敛为止。现在对本文所建立的网络进行BP算法推导。其中a1、b1为隐含层第i个神经元的输出和阈值，a2 、b2为输出层的输出和阈值，w1j 为隐含层第j个输入到第i个神经元的权值，w2li为输出层第i个输入到输出神经元的权值，f1、f2分别为隐含层和输出层的激励函数，pj和t 分别为输入样本和目标输出。

信息的正向传递

隐含层神经元的输出为：

 

数据