线性预测及其Matlab实现

线性预测分析是现代语音信号处理中最核心的技术之一，为现代语音信号处理的飞速发展立下了赫赫功劳，在语音分析、合成、编码、识别等方面都有着广泛的应用，至今仍是最有效的语音分析技术之一。如VoIP和H.323网上多媒体通信系统中所使用的G.729 CS-ACELP语音编码算法就是一种以共轭代数码本激励线性预测为基础的高质量的语音编码标准。

　　1线性预测的基本原理

　　在语音信号处理中最常用的模型是全极点模型。线性预测所包含的基本概念是，通过使实际语音抽样和线性预测抽样之间差值的平方和达到最小值，即进行最小均方误差的逼近，能够决定惟一的一组预测器系数。如果一个随机过程用一个p阶全极点系统受白噪声激励产生的输出来模拟，设这个系统的传递函数为：

　　其中：p是预测器阶数;G是声道滤波器增益。由此，语音抽样s(n)和激励信号e(n)之间的关系可用下列差分方程来表示：

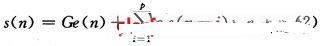
　　即语音样点间有相关性，可以用过去的样点值预测未来样点值。对于浊音，激励e(n)是以基音周期重复的单位冲激;对于清音e(n)是平稳白噪声。

　　在模型参数估计过程中，把如下系统称为线性预测器：

　　式中：ai称为线性预测系数。从而，p阶线性预测器的系统函数具有如下形式：

　　在式(1)中的A(z)称作逆滤波器，基传输函数为：

　　而线性预测方程可以按如下方法得到：把某一帧内的短时平均预测误差定义为：

　　由此可计算出预测系数。

　　由于语音信号的短时平稳性，要分帧处理(10～30 ms)，对于一帧从n时刻开窗选取的N个样点的语音段s(n)，记为Φn(j，i)：

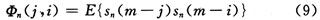
　　2 G.729中线性预测分析的基本原理

　　用10阶线性预测(LP)作短时分析，LP合成滤波器定义为：

　　3在Matlab上实现线性预测

　　3.1加窗和自相关函数计算

　　G.729语音编码算法大多是用C语言编程实现的，程序显得格外冗长，有一定的局限性。由于Matlab在数据分析、自动控制、数字信号处理、绘图等方面具有强大的功能，为了直观的表述，就运用Matlab来实现线性预测分析这一部分的算法。

　　图1给出了混合窗的示意图，它由两部分构成，前半部分是1/2个哈明窗;后半部分是1/4余弦函数：

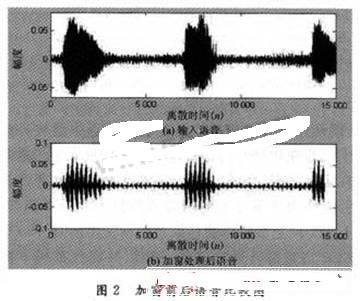
　　式中：有5 ms(40个样点)来自下一帧，15 ms(120个样点)来自上一帧，当前帧10 ms(80个样点)加窗过程如图1所示。

　　得到加窗如图2所示。

　　3.2LP系数的求取

　　求解线性预测滤波器系数ai，将使用到最经典的Levinson-Durbin算法。该算法的步骤为：

　　上面各式中括号内的上标表示预测器的除数。步骤(1)～(4)可对I=1，2，…，P进行递推求解，其中：E为最小均方预测误差;R为自相关系数;k表示反射系数，取值范围为[-1，1];aij表示i阶预测器的第j个系数。通过运算发现，其实在计算过程中，虽然目标是计算一个p阶线性预测器的全部系数，但实际上在递推过程中仅算出了所有除数低于p阶线性预测器的全部系数，同时计算出了最小预测误差能量(递推式中反射系数的取值范围是保证系统H(z)稳定性的充分必要条件，即多项式A(z)的全部根都落在单位圆内)。

　　从推导中得知，φn(j，i)的物理意义可以理解为sn的短时自相关函数。因此，它反映了语音波形的实际情况，即波形不同，值也不同。然而ai的取值由φn(j，i)决定，并随φn(j，i)的改变而改变，因此也可以说ai反映了语音波形的实际情况。

　　其Matlab描述如下：

　　4结语

　　线性预测在语音处理方面的应用很广泛，而用Matlab来实现可以很直观地知道分析结果，为下一步将算法在DSP上的实现奠定基础。