基于上游渐扩管安装条件的内锥流量计性能预测
时间：11-02
来源：互联网
点击：
内锥流量计上游管段（即100MM口径管道）中流体的流速（M/s）；Δｐ为上下游取压点测得的压差值（Pa）。该公式使用伯努利方程进行推导，由于流动中会有能量损失，压力的测量结果也并非为一个平面上的平均压力，并且在实际内锥流量计中，存在低压取压L形立柱的影响，因此，流出系统C往往小于1。
通过点表面积分法，对数值仿真计算结果进行后处理，计算锥体上下游的压力差，并根据公式（4）计算出流出系数。图3即为3种β值在上游渐扩管安装条件下流出系数与雷诺数的关系曲线。
2.4 压力场分析
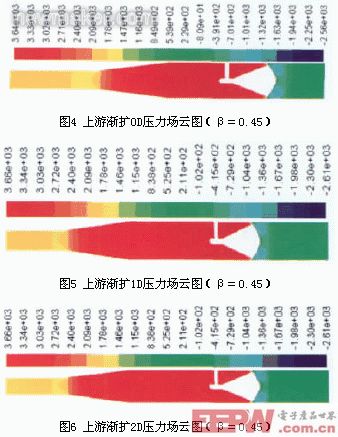
以β＝0.45，入口流速υ＝0.2M/s为例，提取锥体上游和下游局部压力场云图，分析上游不同直管段长度对上、下游压差的影响。压力场云图如图4～6所示。
2.5 数值仿真与实流实验的比较
根据仿真预测结果，针对β＝0.65的内锥流量计，展开了在渐扩管安装条件下的实流实验研究。实验在天津大学流量实验室完成，实验时根据实验装置的现有能力尽可能拓展了雷诺数范围。图7为＝0.65数值仿真与实流实验的C-Re曲线。
2.6 误差来源分析
（1）湍流模型输运各向异性导致预测精度存在差异，另外，在锥体尾部流动出现分离，产生一个较大的旋涡区，而锥体尾部的取压口恰好位于旋涡区中。因此，对旋涡区的计算精度，会直接影响差压值计算的准确度，而差压值与流出系数值直接相关。
（2）本实验中采用RNG k-ε模型，该模型虽修正了湍动黏度，并在ε方程中增加了一项，从而反映了主流的时均应变率，但RNG k-ε模型仍是针对充分发展的湍流是有效的，即是高Re数的湍流计算模型，而在渐扩安装条件下，雷诺数较小，从而限制了预测精度。
3 评价方法与建议的直管段长度
通常将附加不确定度Δσ和平均流出系数相对误差δc珋作为安装条件的主要评价标准。当Δσ与δc珋均小于0.5％时，认为渐扩管安装条件对内锥流量计的影响可忽略，直管段长度适当；当δc珋≥1％或Δσ和δc珋均大于0.5％时，直管段长度不适当；当Δσ、δc珋两者之一远小于0.5％，另一值在0.5％～1％之间，此时直管段长度需谨慎使用。
根据以上评价方法，仿真预测结果表明：β值为0.45，0.65时的上游渐扩管直管段长度为1D；对于0.85的内锥上游渐扩管直管段长度最少为2D。
本研究中，通过仿真预测并对β值为0.65的内锥流量计进行了实验验证，实验根据天津大学流量实验室水流量实验装置的现有能力，尽可能拓展了雷诺数的范围。本研究结果与美国MCC.公司给出的结果进行了对比，如表3。
4 结论
开展了基线实验和上游渐扩实验两类研究，涉及3种节流比，仿真和实验一共进行了15组。将平均流出系数相对误差与附加不确定度作为上游渐扩管对内锥流量计性能影响的主要评价指标。仿真预测结果和实验结果吻合，并与国外相关实验数据进行了对比，给出了不同的研究结论。在本研究雷诺数范围内，研究得出了β值为0.45，0.65所需直管段长度为1D，而β值为0.85所需直管段长度最小为2D的结论。(end)
通过点表面积分法，对数值仿真计算结果进行后处理，计算锥体上下游的压力差，并根据公式（4）计算出流出系数。图3即为3种β值在上游渐扩管安装条件下流出系数与雷诺数的关系曲线。
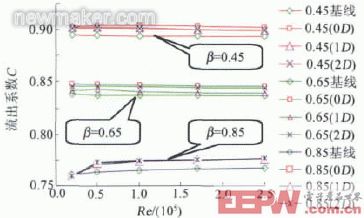
图3 C-Re曲线
2.4 压力场分析
以β＝0.45，入口流速υ＝0.2M/s为例，提取锥体上游和下游局部压力场云图，分析上游不同直管段长度对上、下游压差的影响。压力场云图如图4～6所示。
2.5 数值仿真与实流实验的比较
根据仿真预测结果，针对β＝0.65的内锥流量计，展开了在渐扩管安装条件下的实流实验研究。实验在天津大学流量实验室完成，实验时根据实验装置的现有能力尽可能拓展了雷诺数范围。图7为＝0.65数值仿真与实流实验的C-Re曲线。
图7 仿真/实验C-Re曲线（β＝0.65）
2.6 误差来源分析
（1）湍流模型输运各向异性导致预测精度存在差异，另外，在锥体尾部流动出现分离，产生一个较大的旋涡区，而锥体尾部的取压口恰好位于旋涡区中。因此，对旋涡区的计算精度，会直接影响差压值计算的准确度，而差压值与流出系数值直接相关。
（2）本实验中采用RNG k-ε模型，该模型虽修正了湍动黏度，并在ε方程中增加了一项，从而反映了主流的时均应变率，但RNG k-ε模型仍是针对充分发展的湍流是有效的，即是高Re数的湍流计算模型，而在渐扩安装条件下，雷诺数较小，从而限制了预测精度。
3 评价方法与建议的直管段长度
通常将附加不确定度Δσ和平均流出系数相对误差δc珋作为安装条件的主要评价标准。当Δσ与δc珋均小于0.5％时，认为渐扩管安装条件对内锥流量计的影响可忽略，直管段长度适当；当δc珋≥1％或Δσ和δc珋均大于0.5％时，直管段长度不适当；当Δσ、δc珋两者之一远小于0.5％，另一值在0.5％～1％之间，此时直管段长度需谨慎使用。
根据以上评价方法，仿真预测结果表明：β值为0.45，0.65时的上游渐扩管直管段长度为1D；对于0.85的内锥上游渐扩管直管段长度最少为2D。
本研究中，通过仿真预测并对β值为0.65的内锥流量计进行了实验验证，实验根据天津大学流量实验室水流量实验装置的现有能力，尽可能拓展了雷诺数的范围。本研究结果与美国MCC.公司给出的结果进行了对比，如表3。
表3 仿真/实验研究结果与美国MCC.公司数据的比较
4 结论
开展了基线实验和上游渐扩实验两类研究，涉及3种节流比，仿真和实验一共进行了15组。将平均流出系数相对误差与附加不确定度作为上游渐扩管对内锥流量计性能影响的主要评价指标。仿真预测结果和实验结果吻合，并与国外相关实验数据进行了对比，给出了不同的研究结论。在本研究雷诺数范围内，研究得出了β值为0.45，0.65所需直管段长度为1D，而β值为0.85所需直管段长度最小为2D的结论。(end)
- 上游组合管件对内锥流量计性能的影响(12-03)
- 内锥流量计在氟化氢流量测量中的改进及应用(10-08)
- 差压式流量计系统常见误差解决(01-24)
- 孔板流出系数偏离着重检查问题(01-30)
- 频宽、取样速率及奈奎斯特定理(09-14)
閻忓繐瀚伴。鑸电▔閹捐尙鐟归柛鈺冾攰椤斿嫰寮▎鎴旀煠闁规亽鍔忓畷锟�
- 濡ゅ倹岣挎鍥╀焊閸曨垼鏆ョ€规悶鍎抽埢鑲╂暜閸繂鎮嬮柟瀛樺姇閻撹法鎷嬮鐔告畬缂佸顑呴〃婊呮啑閿燂拷
闁稿繈鍔嶉弻鐔告媴瀹ュ拋鍔呭☉鏃傚Т閻ㄧ姵锛愰幋婊呯懇濞戞挻姘ㄩ悡锛勬嫚閸☆厾绀夐柟缁樺姇瀹曞矂鎯嶉弬鍨岛鐎规悶鍎扮紞鏃堟嚄閽樺顫旈柨娑樿嫰婵亪骞冮妸銉﹀渐闂侇偆鍠愰崹姘舵⒐婢舵瓕绀嬪ù鍏坚缚椤懘鎯冮崟顐ゆ濡増鍨垫导鎰矙鐎ｎ亞鐟�...
- 濞戞搩鍘炬鍥╀焊閸曨垼鏆ョ€规悶鍎抽埢鑲╂暜閸繂鎮嬮柟瀛樺姇閻撹法鎷嬮鐔告畬缂佸顑呴〃婊呮啑閿燂拷
缂侇噣绠栭埀顒婃嫹30濠㈣埖宀稿Λ顒備焊閸曨垼鏆ラ柛鈺冾攰椤斿嫮鎷犻崜褉鏌ら柨娑樺缁楁挾鈧鍩栧璺ㄦ嫚閹惧懐绀夐柛鏂烘櫅椤掔喖宕ㄥΟ鐑樺渐闂侇偆鍠曢幓顏堝礆妫颁胶顏卞☉鎿冧簻閹酣寮介悡搴ｆ濡増鍨垫导鎰矙鐎ｎ亞鐟庨柣銊ュ椤╋箑效閿燂拷...
- Agilent ADS 闁轰焦鐟ラ鐔煎春绾拋鍞查悹鍥у⒔閳诲吋绺藉Δ鍕垫
濞戞挻鎸搁宥夊箳閸綆鍤﹂柨娑樿嫰閸欏繘妫冮姀锝庡敼閻熸瑯鏋僁S闁告艾瀚～鎺楀礉閻旇鍘撮柛婊冭嫰娴兼劗绮欑€ｎ亞瀹夐柣銏╃厜缁遍亶宕濋埡鍌氫憾闁烩偓鍔嶅〒鍫曟儗椤撶姵鐣遍柡鍐ㄧ埣濡法鈧冻缂氱槐鐧咲S...
- HFSS閻庢冻缂氱弧鍕春绾拋鍞查悹鍥у⒔閳诲吋绺藉Δ鍕垫
閻犙冨缁讳焦绋夐幘鎰佸晙闁瑰搫鐗愰鎶芥晬鐏炶棄寮块梻鍫涘灱椤斿骞掗崷娆禨S闁汇劌瀚慨娑㈡嚄閽樺瀚查幖瀛樻⒒閺併倝鏁嶇仦钘夌盎闁告柡鏅滈崑宥夊礂閵娾晜妗ㄧ紒顖濆吹缁椽宕烽弶娆惧妳濞戞梻濮电敮澶愬箵椤″锭SS...
- CST鐎甸偊鍠楃亸婵嗩啅閵夈倗绋婇悗骞垮€曢悡璺ㄦ媼椤撶喐娈岀紒瀣儏椤ㄦ粎鎲楅敓锟�
闁哄瀛╁Σ鎴澝虹€ｂ晛鐦滈悹浣筋嚋缁辨繈宕楅妸鈺傛〃閻犱礁寮跺绶維T闁告艾瀚伴妴宥夊礉閻旇鍘撮柛婊冭嫰娴兼劗绮欑€ｎ亞瀹夐柣銏╃厜缁辨繈宕濋埡鍌氫憾闊浂鍋婇埀顒傚枙閸ゆ粎鈧冻闄勭敮澶愬箵椤″T閻犱焦宕橀鍛婃償閺冨倹鏆�...
- 閻忓繐瀚伴。鍫曞春閾忚鏀ㄩ柛鈺冾攰椤斿嫮鎷犻崜褉鏌�
濞戞挸娲ｇ粭鈧Δ鍌浬戦妶濂哥嵁閸愬弶鍕鹃悹褍鍤栫槐婵囨交濞嗗海鏄傞悹鍥у⒔閳诲吋绋夋潪鎵☉闁革负鍔岄惃鐘筹紣閹寸偛螚闁哄牜鍨堕。顐﹀春閻旀灚浜ｉ悘鐐存礃鐎氱敻鎳樺鍓х闁瑰灚鎸风粭鍛村锤濮橆剛鏉介柣銊ュ缁楁挻绋夊顒傚敤缁绢厸鍋�...
- 鐎甸偊鍠楃亸婵堜焊閸曨垼鏆ユ繛鏉戭儔閸ｆ椽骞欏鍕▕闁糕晝顢婇鍕嫚閸撗€鏌ら柛姘墦濞夛拷
閻犳劦鍘洪幏閬嶅触閸儲鑲犻柡鍥ㄦ綑閻ゅ嫰骞嗛悪鍛缂傚啯鍨甸崹搴ㄥΥ娓氣偓椤ｅ墎鎷崣妯哄磿闁靛棔鑳堕妵姘枖閵忕姵鐝ら柕鍡曟娣囧﹪宕ｉ柨瀣埍闁挎稑鏈崹婊呮啺娴ｅ湱澹夐柡宥夘棑缁ㄥ潡鏌呴敓锟�...
栏目分类