基于上游渐扩管安装条件的内锥流量计性能预测

引言

内锥流量计在许多方面表现出比传统节流式流量计更为出色的性能，但内锥流量计尚未标准化，对其安装条件的研究成了国内外讨论与关心的热点。STEpHEN A.IFFT等人利用实验方法先后研究了上游单个90°弯头与不在同一平面的、前后紧接的双90°弯头以及全开和半开阀门对内锥流量计关键参数的影响；此后，S.N.SiNgH，R.J.W.PETERs先后对内锥流量计的抗流场扰动性能开展了实验研究；李彦梅等人利用数值仿真和实流实验相结合的方法研究了上游单弯头和双弯头安装条件对内锥流量计性能的影响。天津大学的流量实验室先后对内锥量计流出系数、可膨胀系数及湿气测量等方面展开了研究，并取得了宝贵的经验成果。

近年来，国内虽然掀起了推广应用内锥流量计的热潮，但对内锥流量计的关键技术指标、安装条件未进行相应的标定，大多直接沿用美国MCC.公司的产品说明书。针对100MM口径、β值分别为0.45，0.65，0.85的内锥流量计，开展了在渐扩管安装条件下基线及上游不同直管段长度的仿真研究，并做了一定的实验验证，预测了上游渐扩管安装条件下的内锥流量计所需的最短直管段长度。

1 建模与研究方案设计

1.1 内锥流量计的几何结构

内锥流量计的结构如图1所示。内锥体可以看作是两个底面积相同的圆台拼接而成，通过支架固定并与管道同轴，上游直接在管壁取压，下游采用锥尾取压方式，锥尾的压力通过锥体内导压孔和支架中的测量管传递到管壁取压孔。

1 前端取压口；2 尾部取压口；3 管壁；4 支架；5 锥体
图1 內锥流量计几何结构

1.2 研究方案设计

对100MM口径、β值分别对0.45，0.65，0.85的内锥流量计开展在上游渐扩管安装条件下的数值仿真，然后针对β值为0.65的内锥流量计进行实流测试，管内径100MM定义为1D。为保证管内流体流动为充分发展的湍流状态，物理实验样机上游直管段100D，仿真实验样机上游直管段10D。其中，渐扩管安装条件为：DN50的圆型管道经过渐扩管（长200MM）与DN100的圆型管道相连。设计方案如表1。

表1 研究方案设计（研究介质：常温水）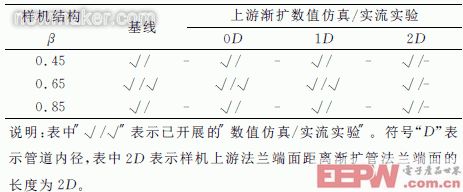

2 数值仿真

2.1 几何模型与网格剖分

仿真几何模型利用Gambit2.2.30软件建立，采用三维方式建模以保证数值仿真几何模型与物理实验样机完全一样。流量计主体管段长400MM，在渐扩管的前端设有10D直管段，流量计后方直管段长10D。为更准确地获得锥体附近压力的变化情况，在网格剖分时，采用size函数，对锥体附近的网格进行细密的划分，而远离锥体的上、下游直管段区域网格逐渐变得稀疏，网格类型为四面体，网格单元数量约60万。三维几何模型与网格剖分如图2所示。

图2 内锥流量计三维模型及网格剖分（局部）

将网格文件导入FLUENT6.3.26软件后，为优化网格结构，减少网格数量，提高计算效率，首先将网格类型转换成六面体，然后利用分离式求解器进行求解，仿真介质为常温水。入口条件为速度入口和流出出口；流速为0.5～5M/s；并采用标准壁面函数法对近壁区进行处理，壁面为无滑移条件。

2.2 湍流模型与边界条件

对比目前常见的湍流模型，标准k-ε模型在科学研究及工程领域获得了最广泛的检验与成功应用，但当应用于强旋流、弯曲壁面流动或弯曲流线流动时，会产生一定的失真。杨胜等在对汽车外部流场仿真研究中，比较了spalart-Allmaras-方程模型、标准k-ε模型、RNG k-ε模型、Realizable k-ε模型和RsM模型的预测结果后，认为RNG k-ε模型的预测性能要强于其余的4种模型。因此研究中采用RNG k-ε模型计算流场，利用有限体积法实现控制方程的离散化，采用sIMPLE算法进行求解。根据GAN等的研究，在仿真时，除压力项采用二阶迎风格式外，其余都利用了QuiCk格式进行离散。亚松弛因子采用FLUENT软件的默认值，实践证明其收敛效果比较好，残差收敛精度设为10-5。计算时选取5个流速点，方向取入口面的法线方向。其中100MM口径内锥流量计仿真湍流参数如表2所示。

表2 100MM口径内锥流量计仿真湍流参数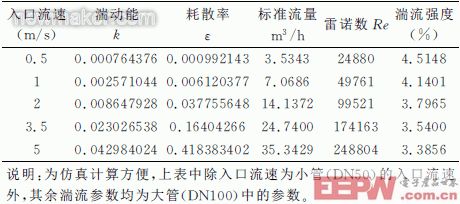

湍流参数计算如下：

（1）湍动能k求解

式中，uavg为平均速度；I为湍流强度。

湍流强度依据经验公式进行计算

式中，uavg为脉动速度的均方根；ReDH为以管径为特征尺度计算的雷诺数。

（2）湍流耗散率ε的求解

式中，Cμ为湍流模型中指定的经验常数，一般取0.09；而L为湍流长度尺度，与管道内径L的关系为l＝0.07L。

2.3 计算结果

流出系数C是内锥流量计的关键参数之一，对于不可压缩流体，流出系数C定义为內锥流量计中实际流量与理论流量的比值。根据能量守恒定律和质量守恒定律，可以推导出C的计算公式为

式中υ是流动稳定的情况下