基于灵敏度分析和GA的模拟电路故障诊断

tave与fitmax越接近，种群个体越集中[8]。

为之后的新一代使用的交叉概率。经过变换之后无法保证其值在0~1之间。同理，也无法满足区间要求。实验证明，在算法运行过程中、值的变化超出了[0,1]，会导致算法无法运行。

在以上算法的思想基础上，本文提出一种改进的自适应遗传算法。显然，的变化范围必然在(0,1]区间内。、值随变化而变化，但需确保其值控制在(0.1)区间。本文提出如下公式

其中a,b,c,d为一个较小系数，根据所需控制的、 的范围来进行相应的修改。它符合遗传算法对、的变化要求。当时种群越分散，此时、的变化缓慢，时，种群越集中，、急剧增加来提升获得新个体的速率。

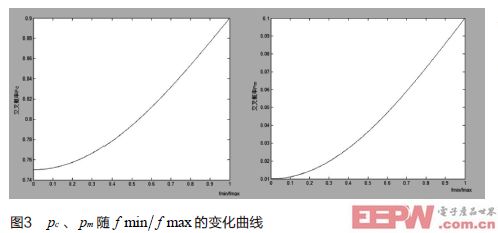
根据之前求出的诊断率较高的范围，本文选择将的范围控制在[0.75,0.9]区间、在[0.01,0.1]区间，故有

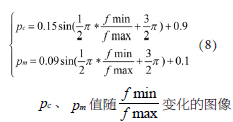
值随变化的图像分别如图3所示。

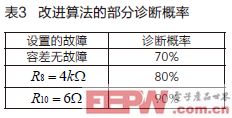
将改进的自适应遗传算法应用于之前故障诊断率较低的R1、R3小故障诊断中，遗传代数增加为5000代。其余设置不变，发现算法诊断率大大增加。在实际检测中，可采用上述改进算法诊断，将算法运行多次，将参数偏差最大，偏差次数最多的元件定位为故障元件，即可准确的定位故障元件。

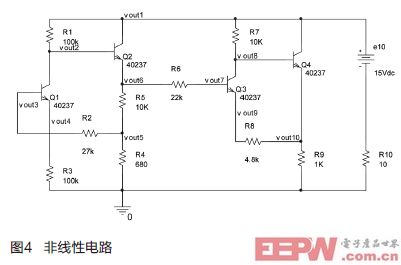
将改进后的自适应算法应用于非线性直流电路的软故障诊断，电路如图4所示。该电路共有10个电阻R1~R10，10个电压测试点vout1~10。

　　5 结论

改进后的自适应遗传算法适用于直、交流线性电路，直流非线性电路，实验结果证明大大提高了故障诊断概率。与其他算法相比，该算法不仅适用于单软故障，同时也适用于多软故障的检测，且大电路检测中仅需测得测试点电压值，输入程序中即可得出结果，诊断速度非常快。对于故障元件参数偏差超过20%的多软故障，该算法诊断概率较高。故障元件参数偏差在10%~20%时，由于本身元器件容差设定在±10%，其模糊性导致故诊断概率较低。故针对于偏移量较小的多软故障方面的检测率还有待提高。

　　参考文献：

[1]李焱骏.以电压灵敏度向量为故障特征的模拟电路软故障诊断方法研究[D].电子科技大学,2009

[2]周龙甫,师奕兵,李焱骏.容差条件下PSO算法诊断模拟电路单软故障方法[J].计算机辅助设计与图形学学报,2009,21(9):1270~1274

[3]Wang P,Yang S Y.A new diagnosis approach for handling tolerance in analog and mixed signal circuits by using fuzzy math[J].IEEE Transactions on Circuits and System—I：Regular Papers,2005,52(10):2118~2127

[4]Gao Y,Xu C,Li J.Linear programming relax—PSO hybrid bound algorithm for a class of nonlinear integer programming problems[C].Guangzhou:Proceedings of International Conference on Computational Intelligence and Security,2006:380~383

[5]Whitley D,et al.Genitor II:A distributed genetic algorithm [J].J Expt. Ther. Intell,1990,2: 189~214

[6]吴喜华,谢利理,葛茂艳.基于GA-LMBP算法的模拟电路故障诊断方法[J].现代电子技术, 2010(4):177~179

[7]Srinivas M,Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEETrans On System, Man and Cybernetics, 1994, 24(4): 656-667

[8]韩瑞锋.遗传算法原理与应用实例[M].北京:兵器工业出版社,2010:60~66

[9]刘洲洲.基于遗传算法的足球机器人路径规划[J].电子产品世界,2013(2):28~29