基于灵敏度分析和GA的模拟电路故障诊断

当今电子设备的迅猛发展对电子设备的故障检测提出了更高的要求。为了准确定位故障元件，提出了通过灵敏度估算故障元件偏差值来寻求电路故障元件。电路网络C中共有m个元件，w个节点，其中有n个可测节点电压V1、V2……Vn。其中独立电源及参考地都在网络C中，假设端口i处有一故障元件xi。当元件发生故障时，xi转化为xi+Δxi。k处输出电压由Vk转化为Vk+ΔVk [1]。当有容差且多个故障元件时，根据节点电压灵敏度定义可得

断方程。

　　1 诊断方程的转化

当电路中器件参数值发生小的偏移，单软故障发生的概率较大[2]。Q1、Q2 ……Qm为各元件参数偏移百分数，引入自变量方程

引入罚因子M，将有约束的线性规划问题转化为无约束条件的极值求解问题[3-4]。

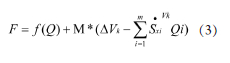
式中为PSpice内定义的相对灵敏度，为故障元件i的偏移百分数，为电压输出点k处估算的变化量。

　　2 遗传算法求解实例分析

采用遗传算法求解F的极小值。故障诊断电路采用与文献[3]、[4]中相同的直流电路。

测试数据通过在PSpice中将标称电路修改为容差下的故障电路进行MC仿真获得。将其中一组数据作为测试数据输入程序中。实验中设置故障R1=0.5。各个元件参数的偏移百分数作为算法搜索的种群，以F为目标函数。设置连续多代算法群体均值偏差小于某个较小值L或者遗传代数达到设置值，算法即终止。

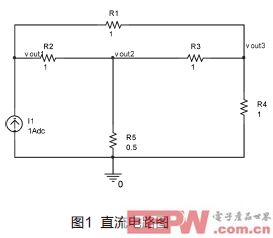
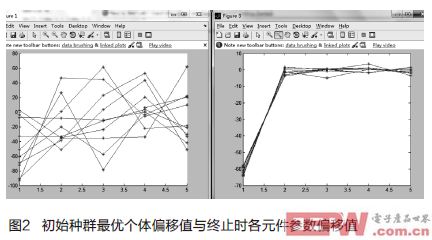
随机产生种群初始值，用同一个测试样本重复进行10次模拟电路故障诊断，数据结果输出如图2，左边是运行十次算法中，随机产生的初始种群里最优个体元件参数偏移值的分布图。右边是算法收敛后停止时的最优个体元件参数偏移值的分布图。从图中可以看出十次算法运行过程中有九次算法收敛，检测到故障。并较为准确的给出了各元件参数偏移值。其中有一次没有收敛，因满足遗传代数而终止搜索。图中X坐标为R1-R5元件，Y坐标为各元件参数偏移百分比，单位为%。

将容差故障电路进行20次蒙特卡洛分析，输出的一次分析中三个测试点电压值为一组测试数据，每组数据输入并进行一次遗传算法搜索。求其20个测试数据下的诊断率。Mut为较小的数，M为很大的正数，诊断率可达94%以上。某次参数设置后用20次MC分析的结果作为测试数据进行诊断。本文的结果1与文献[3]、[4]的方法的诊断结果2、结果3进行对比，得出表1。

　　3 遗传算法的改进

搜索最适合的遗传算子，进一步提高诊断概率。同电路设置故障元件R1偏移-15%，电阻容差为±5%。在初始种群生成时，设定每个个体为单软故障的参数。生成的Chrom为各个元件参数偏移百分数，则元件参数变为R(1+x%)。R表示元件标称值，x为随机产生的偏移百分数，单位为%。但经过交叉变异等操作之后的新的种群即可能完全随机变化，可为多软故障。当运行到终止代数或满足阈值条件即终止算法。阈值设置为相邻两代的E

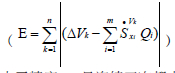
的差值小于精度L，且连续三次都小于精度L，则认为达到了最优点。

实验可得变异率较大的其种群均值分布差异较大。而变异概率减小时，种群均值变化较小，其值容易陷入局部最优解。本文将交叉算子与变异算子在一定范围内以一定的步长变化，筛选出结果较好的取值，然后统计各个算子出现的概率来判别算子的最优取值范围[5]，同时，设置遗传代数逐步增加。实验结果得出变异率在0.01~0.02之间，交叉率在0.7~0.95之间所占输出比例最大。表2为设置变异率为0.01，交叉率为0.85，遗传代数为100时设置故障及诊断概率。

由于故障的模糊性，小故障诊断率较低，增加遗传代数提高了收敛率，但并没有很好的提高诊断概率。以下为检测R3时，算法收敛时得到的一组数据，该数据并没有检测出正确的故障，Q1：6.4529，Q2： -5.5277， Q3 ：-0.0268，Q4：3.2115，Q5 ：-1.9950。其中R1、R2同时为故障元件时的输出与设置的故障R3=0.8 等效，所以在具有模糊性的故障诊断中，诊断率相对较低[6]。

　　4 动态自适应遗传算法，提高诊断概率

M. Srinivas提出的自适应遗传算法是当群体适应度比较集中时，适当增大Pc、Pm的值，而当群体适应度较为分散时，适当减小Pc、Pm的值，对编码当中每一位都根据Pc、Pm来选择是否进行交叉和变异操作[7]。但是该算法以个体为单位来考虑，缺乏整体的考虑。算法易陷入局部最优。同时在对每个个体计算Pc、Pm的值会降低算法执行的效率。

文献[8]中韩瑞锋提出的算法是利用群体最大适应度fitmax，最小适应度fitmin，适应度平均值fitave这三个变量来控制Pc、Pm的值。其中fitmin与fitmax越接近，越容易陷入局部最优，fitave与fitmax反映了群体内部适应度的分布情况，fi