基于MSP430与FPGA的多功能数字频率仪设计*

频处理和低频处理三个部分。对于高频处理部分，待测信号的频率较高，正弦波无需整形为方波也可视为上升沿，只需进行高增益的放大;低频处理部分先经过放大电路，再经过史密斯触发器整形为方波;中频处理部分先经过放大电路，再经10分频电路后送入低频处理部分的整形电路，从而输出方波。本系统采用TI公司宽带超低噪声电压反馈运算放大器OPA847搭建前级信号放大电路，该芯片带宽增益积可达3.9GHz，电压输入噪声低至，压摆率高达950V/μs。

2 系统实现

MSP430主程序流程图如图4所示，主要包含正弦波频率、两路方波间隔时间和矩形脉冲占空比的测量功能。当按下相应按键时，MCU将向FPGA发送控制信息，使其开始相应参量的测量。当测量结束时，FPGA将测量值通过SPI通信方式传输至MCU中，MCU进行最终计算并显示在OLED12864上。由于FPGA的系统时钟较快，MCU的系统时钟相对较慢，因此，设置MCU为SPI通信的主设备，FPGA为从设备。MCU采用I/O口模拟SPI的模式，由I/O口产生时钟信号SCLK，从而实现FPGA与MCU的数据互传。

FPGA模块主要包含顶层文件、测频模块、高电平时间测量模块、低电平时间测量模块、SPI通信模块和时间间隔测量模块等。其中，FPGA晶振产生初始系统时钟，经锁相环按一定系数倍频后为各模块提供时钟信号。MCU通过两根控制线对频率、占空比、时间间隔三种功能进行选择。待测频率的正弦波信号或待测占空比的方波信号经过输入调理电路后都将调理为性能良好的方波信号，该路信号直接与FPGA的测频模块、高电平时间测量模块、低电平时间测量模块相连，从而得到该路信号的频率和占空比。测量两路方波信号时间间隔时，两路输入信号通过输入调理电路的两级放大后，任一路经过1.5倍分频后与第二路信号一同接入时间间隔测量模块，实现对两路等频率、等占空比方波信号超前或滞后情况下时间间隔的测量。

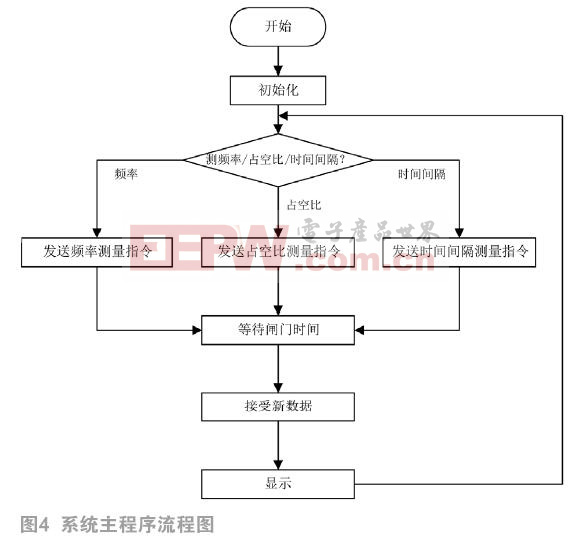
3 测试结果与分析

数字频率仪的性能主要取决于测量的精确度、高精度的频率范围、输入电压的幅度值等。频率范围越大，输入电压幅度越低，实现高精度测量越困难。本系统设置FPGA的同步时间为1s，目标频率测量精度高于0.01%，则有：

(12)

因此，设置FPGA锁相环倍频系数为5，将40MHz的初始时钟脉冲倍频至200MHz，以满足系统测频精度需求。为了验证本测量系统的稳定性及测量结果准确性，进行了七组试验。

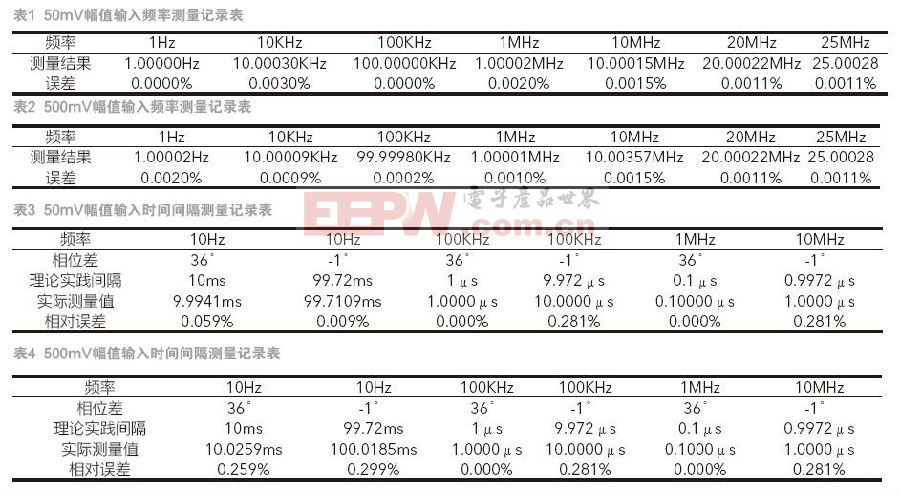
首先，在50mV及500mV下，1Hz～25MHz频段范围内，对不同频率值的正弦波进行频率测试，测试目的是验证本系统正弦波频率测量功能的准确性，测试结果如表1及表2所示。从测试结果可知，在1Hz～25MHz频段内，本系统测量结果的相对误差最大值为0.0020%。

在50mV及500mV下，10Hz～10MHz频段范围内，对时间间隔为0.1μs～99.72ms的两路方波信号进行时间间隔测试，测试目的是验证本系统时间间隔测量功能的准确性，测试结果如表3及表4所示。从测试结果可知，时间间隔测量结果的相对误差最大值为0.299%。

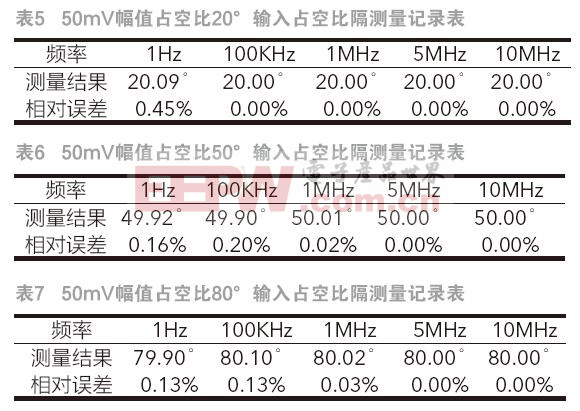
在50mV下，对1Hz～10MHz频段范围内的矩形脉冲信号进行占空比测试，测试目的是验证本系统矩形脉冲占空比测量功能的准确性，测试结果如表5、表6及表7所示。从测试结果可知，本系统在该情况下测量结果的相对误差最大值为0.45%。

通过以上7 组试验充分检验了系统正弦波频率测量、两路方波信号时间间隔测量、矩形脉冲占空比测量功能的准确性及稳定性，正弦波频率测量相对误差不超过0.0020%，两路方波信号时间间隔相对误差不超过0.299%，矩形波占空比相对误差不超过0.45%，操作过程极为方便，能实现量程的自动切换，具有高精度、高稳定性的特点。

4 结论

针对高精度多功能测频的需求，本文提出了基于MSP430与FPGA的多功能数字频率仪，并实现进一步优化标准时钟信号频率的设置。该系统可以实现正弦波频率测量、矩形波占空比测定、两路方波信号时间间隔检测等功能。测试结果表明，该系统完全达到了预定的设计功能，并具有高精度、高稳定性的特点。本设计部分功能仍有待进一步提高与完善，理论上，本测频方法可实现0Hz~200MHz的精准测频。本文尚未对25MHz以上高频输入调理电路的有效放大及1Hz以下低频整形电路的高速整形提出解决方案，尚具有进行功能性完善的空间，届时将具有更好的实际应用价值。

参考文献：

[1]张天恒,叶伟,王阳阳,等. 基于SOPC的便携式高精度频率仪设计[J].仪表技术与传感器,2015,05:34-37.

[2]易龙强. 基于一元线性回归理论的数字正弦信号频率测量算法[J].电测与仪表,2011,03:20-24.

[3]许珉,刘晓辉,王玺,等. 基于加四项Nuttall窗递推DFT插值算法的高精度测频方法研究[J].郑州大学学报(工学版),2