时钟抖动的定义与测量方式

1简介

抖动是实际信号的一组边沿与理想信号之间的偏差（兔子：说白了，抖动就是实际情况和理想情况不一样，差别越大抖动越大）。时钟信号的抖动通常由系统中的噪声或其他干扰因素引起。影响因素包括热噪声、电源变化（波动）、负载的状况（负载也可以反过来影响时钟信号）、设备噪声和临近电路耦合进来的干扰。

2抖动的分类

抖动可以通过许多方式测量（不同方式测量到的抖动被分别加以定义），以下是主要的抖动分类：

1. 周期抖动（Period Jitter）

2. 相邻周期间的抖动（Cycle to Cycle Period Jitter）

3. 长时间抖动（Long Term Jitter）

4. 相位抖动（Phase Jitter）

5. 单位时间间隔抖动（TIE，Time Interval Error）

2.1周期抖动

周期抖动是时钟信号的实际周期长度与理想周期长度之间的偏差，测量样本为数目不定（随机）的一组周期。如果给定一定数目的单个时钟周期，我们就可以通过测量每个周期的长度并计算平均的周期长度，以及这些时钟周期的标准差和峰峰值（peak-to-peak value）。这里所说的标准差和峰峰值也分别被称为RMS抖动和Pk-Pk周期抖动。

许多文献将周期抖动直接定义为被测时钟周期与理想周期之间的误差。但是真实情况下很难对理想周期进行量化。如果我们用示波器观察一个标称100MHz的晶振，测得的平均时钟周期却可能是9.998ns，而不是理想的10ns。所以退而求其次，通常将平均周期作为理想周期看待（兔子：因为实际周期都是在理想值周围按照一定规律分布的，如果测量时间足够长，得到的平均值就可以非常接近理想值）。

2.1.1周期抖动的应用

周期抖动对于计算数字系统的时序裕量十分有用。假设在一个基于微处理器的系统中（上升沿采样），处理器要求1ns的数据建立时间（即数据需要在时钟上升沿1ns前保持稳定有效）。当时钟的某个周期抖动为-1.5ns时，上升沿会出现在数据有效之前，如此处理器将会采集到错误的数据。如图1所示：

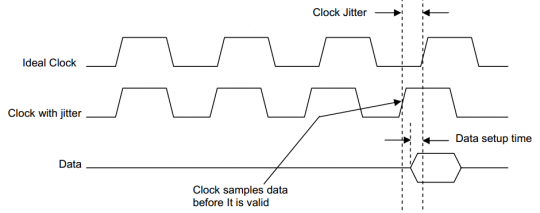
图1时钟抖动造成的数据建立错误

类似的，如果另一个处理器需要2ns的数据保持时间，但是时钟某一个周期的抖动是+1.5ns，那么实际有效的数据保持时间只有0.5ns，处理器也会采到错误的数据。如图2：

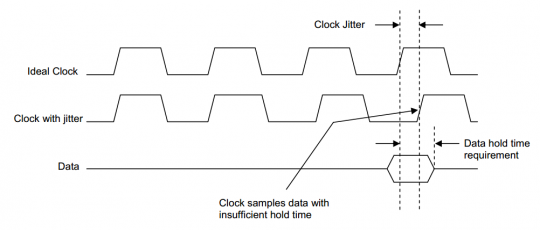
图2时钟抖动造成的数据保持错误

2.1.2由RMS抖动计算Pk-Pk抖动

由于时钟的周期抖动是随机的，并遵循高斯分布。因此周期抖动完全可以用统计学中的均方根（RMS ，Root Mean Square，别说不会算）来表示，单位为皮秒（ps）。但是呢，峰峰值却和计算建立保持时间裕量有更大的联系（峰峰值表示了最大误差，超过建立保持时间要求，数据采样就有可能出错）。要将10000个时钟周期的RMS抖动换算成Pk-Pk抖动，可遵循以下等式：

Pk-Pk周期抖动=7.44 x RMS抖动 *等式1

例如：若RMS抖动为3ps，则Pk-Pk周期抖动为7.44 x 3 = ±11.16ps。

等式1其实是由高斯概率密度函数表（PDF ，Gaussian Probability Density Function）推导出来的。比如当样本个数为100时，从统计学的平均情况来讲，其中 99个会落在有效值周围的±2.327σ范围内，只有1个会落在该范围之外。根据JEDEC标准的要求，某司测量RMS周期抖动时设定的样本数为10000。

表1高斯概率密度函数表（PDF）

2.1.3周期抖动测量方式

JEDEC Standard 65B中将周期抖动定义为某一随机数量的时钟周期与理想周期之间的偏差（由定义了一次，生怕大家忘了）。JEDEC标准进一步地指定了测周期抖动需要测量10000个信号周期（多一个少一个应该也无所谓吧）。某司推荐的测试步骤如下：

1. 测量一个时钟周期（一个上升沿到下一个上升沿之间）的长度，即一个样本

2. 等待随机个时钟周期

3. 重复1、2两步10000次

4. 通过测到的10000个样本，计算平均值，标准差(σ)，和峰峰值

5. 重复1-4步骤25次，通过这25组结果，计算平均峰峰值

10000个随机样本计算出的标准差（σ），即均方根（RMS，也有人认为均方根和标准差并非等同）已经很精确了，RMS的误差可以通过如下等式计算：

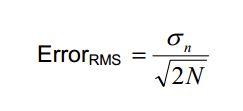*等式2

等式中的σn为样本的RMS，N为样本数。

例如：样本数为10000，RMS误差为0.0071 σn。这种误差是随机的，并且遵从高斯分布，通常用±3 x RMS误差来计算最大测量误差。

又例如：如果从10000个样本中计算出RMS为10ps，