基于机载平台的干涉仪测向技术研究
天线盘的孔径,以提高阵列的分辨力。
2.2 四阶累积量2D-MUSIC
2.2.1 四阶累积量2D-MUSIC的阵列扩展特性及原理
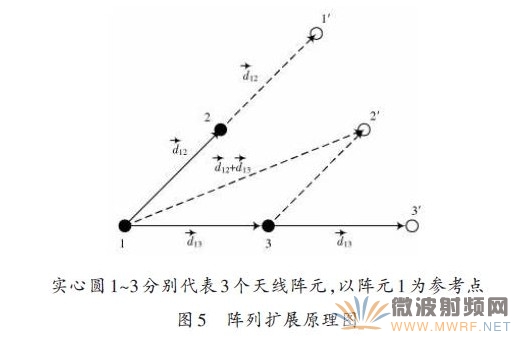
王永良等人给出了四阶累积量特性的详细理论推导,这里不再重复阐述。如图5所示,以空间中3个天线阵元为例,对四阶累积量的阵列扩展特性进行说明。
其阵列导向矢量可以表示为:
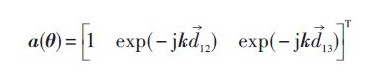
式中:k 表示辐射信号入射角度矢量;d12和d13分别代表阵元2.3相对参考阵元1的位置矢量。
利用四阶累积量的扩展特性对图5 的阵列扩展后的导向矢量为:
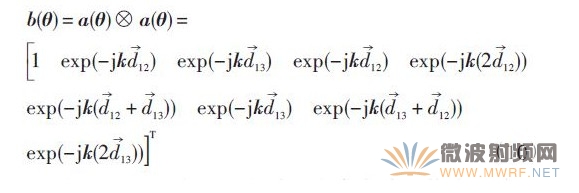
由图5可以看出,空间中3个真实阵元构成的阵列经四阶累积量阵列扩展后构成了6个阵元的虚拟阵列,阵列孔径扩大1倍,然后利用扩展后的阵列对辐射信号的入射角度进行估计,以达到提高分辨力的效果。
基于四阶累积量的MUSIC算法也是利用信号子空间与噪声子空间的正交性,其空间谱函数表达式为:
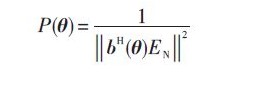
通过谱峰搜索,找到P个极大值对应的角度,实现对辐射信号的二维DOA估计。
仿真分析4:
以均匀5元椭圆阵为例验证四阶累积量的MUSIC算法和MUSIC算法分辨性能,同样采用的信噪比为20 dB,快拍数为1 000,取三个辐射信号(45°,75°),(45°,80°),(38°,30°),仿真结果如图6所示。
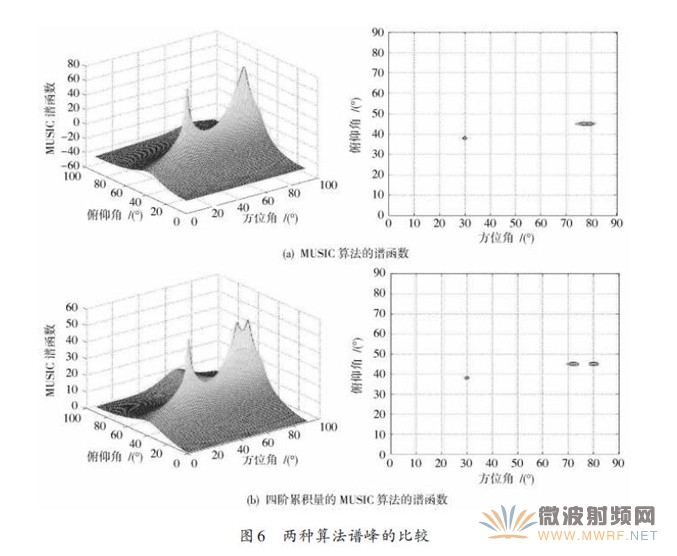
由图6(a)可以看出,采用MUSIC 算法对入射角度于(45°,75°),(45°,80°)进行估计失败,而采用四阶累积量MUSIC算法进行估计时得到了两个尖锐的谱峰,通过四阶累积量MUSIC 算法的谱函数搜索得到入射角度为(45°,75.5°),(45°,80°)。由此可见,采用四阶累积量MUSIC算法使得阵列孔径得到了有效的扩展,其分辨力高于MUSIC算法。
2.2.2 四阶累积量2D-MUSIC算法与MUSIC算法计算量分析
MUSIC算法通过对接收数据的协方差矩阵和进行特征分解,运算量为ο(M2 K) + ο(M3)。计算一个四阶累积量需要9L次复乘运算,其中L表示快拍数,奇异值分解的计算量约为ο(M6),其中M表示所构造的累积量数据矩阵的维数。其实从四阶累积量MUSIC 算法阵列扩展原理图可知,采用该算法进行谱峰搜索所用的阵元个数远远的多于原阵列的阵元个数。譬如在图6(b)的仿真实验中,需要对方位角0~360°,仰角0~90°范围内进行谱峰搜索,那么将方位角和仰角的搜索步长分别设置为1°,0.5°,则需要361 × 181次谱函数计算,而谱函数计算量与阵列导向矢量有关,即与阵元数量有关。也就是说虽然四阶累积量MUSIC算法引入虚拟阵元扩大孔径使得分辨力提高,但也导致谱峰搜索的计算量大增。
仿真分析5:
计算量仿真统计分析。对不同快拍数下这两个算法所占用的计算时间进行统计,各算法计算时间均由100次Monte-Carlo实验进行平均得到,见表1.
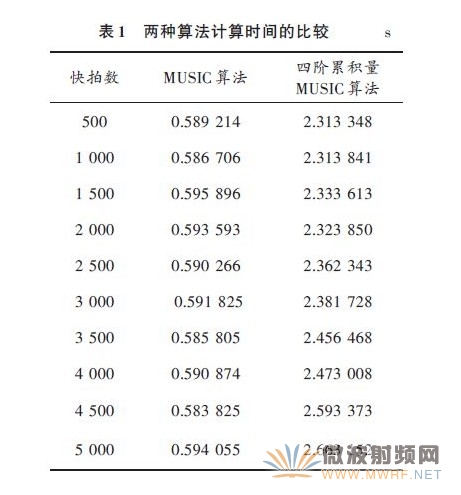
由表1可以看出,四阶累积量MUSIC算法的计算时间大约是MUSIC 算法的4 倍。但文献[5]中从算法的角度给出了一种快速去冗余的方法,将M2 × M2 的四阶累积量矩阵转化为(2M – 1) × (2M – 1)的四阶累积量矩阵,从而大大降低了计算量。同时相信随着DSP 和FPGA 等数据处理飞速发展,四阶累积量MUSIC算法的运算时间会减小,从而更好的将四阶累积量MUSIC算法应用于阵列信号处理中。
3 结语
根据机载干涉仪测向系统面临着可供布阵的空间有限,不能像陆基一样布阵成理想阵列,考虑到飞机机身横向较窄而纵向很长给出了椭圆阵列模型,通过仿真分析了椭圆孔径与波长之比对入射角度的估计性能,发现了测向精度受阵列有效孔径的限制。然而在实际机载测向系统中通过增大阵列孔径来提高分辨力估计性能是不现实。考虑通过四阶累积量阵列扩展特性来引入虚拟阵元,这样就可以在受限平台上实现天线盘孔径大增,完成一。二维DOA高精度估计。惟一的缺点就是计算量大,所以今后的努力方向是不仅要从改进算法的角度来减少四阶累积量的运算量,也从用DSP来实现的角度缩短执行时间。
