基于机载平台的干涉仪测向技术研究

0 引言

随着航空电子侦察技术的发展，机载测向系统以其作用范围大。侦测距离远。机动性强和可实现单机对地面目标定位等优点，能够完成地面通信电子战设备所不能完成的远距离。大区域作战任务，正越来越受到国内外关注。但是在实际工程应用中，机载测向中面临着以下几个方面的问题。

(1)机载平台可供布设天线阵列的有效空间。允许的天线阵元尺寸和数量十分有限，不能使用大基础天线阵;同时飞机结构面多为弧面，这也限制了均匀圆形阵向低频段扩展的可能。本文考虑到飞机本身的结构特点是机身横向窄纵向长，为有效利用飞机机腹的空间，提出了均匀椭圆布阵的形式，通过仿真分析了椭圆阵列孔径与波长之比对入射角度的估计性能影响。

(2)现代雷达系统，通常采用在目标雷达周围配备有源诱饵进行保护，这就要机载测向系统有高的分辨力，但是基于相位干涉仪的测向方法只能实现对单个信号的测向，而空间谱估计测向法可以实现对一个波束宽度内多个入射信号的来波方向估计，所以有效地提高空间谱估计方法在实际测向系统中的分辨力至关重要。

(3)在实际测向中天线阵列通道幅相失衡。天线阵元的互耦等会导致测向性能的下降，所以亟需采用有效的校正方法来改善测向性能。

本文重点研究前两个方面的问题。

1 机载平台测向天线阵设计

1.1 相关干涉仪测向技术

测向原理如下：在测向天线阵工作频率范围内和0~360°方向上，各按一定规律设点，同时在频率间隔和方位间隔上建立样本群，在测向时，将所得的数据和样本群进行相关运算和差值处理，以获得来波信号方向，可以实现宽频带范围内无模糊测向，对阵列的摆放形式没有特殊要求。

基于相位差拟合的相关干涉仪代价函数为：

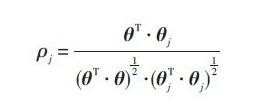
式中：θ为观测相位差向量;θj为对应于(θ，φ)方向的相位差向量，使得ρj最大值所对应的原始相位样本值就是实际入射信号的方位。

1.2 测向天线阵设计及仿真

针对机载平台的特点，给出了椭圆天线阵列摆放示意，如图1所示。

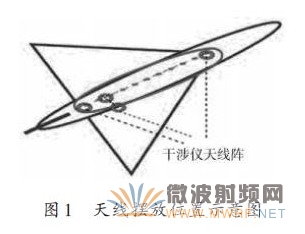
设M个天线阵元均匀分布在一个椭圆圆周上，以几何中心为参考点，则阵列的方向向量a(θ)可表示为：

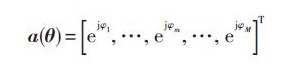
设a(θA)，a(θB )是均匀椭圆阵列上的2个方向向量，则相关系数为：

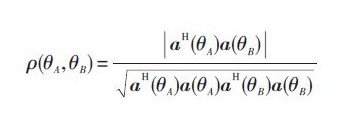
仿真分析1:

设椭圆阵孔径与波长之比(d λ)分别为12和14,信号入射方向为50°，5元均匀椭圆阵的相关系数图如图2所示。

可见，相关系数的最大值在方位角50°处。从仿真图2可得如下结论：d λ越大，主瓣越窄，方位测量精度越高;去除测向模糊就是要求相关系数图的主瓣与副瓣的高度易于分辨。MUSIC算法其分辨力与阵列孔径成正比。也就是说当可利用的阵列孔径受限时，会影响到分辨力，但为了提高系统的分辨力而增大天线盘的孔径代价太大。所以要在不需要通过增大阵列的物理孔径来实现MUSIC算法的分辨力上下功夫。

2 MUSIC算法分辨能力2.1 MUSIC算法原理及分辨性能设有P个不相关窄带入射到M元远场线阵上，则阵列输出向量为：

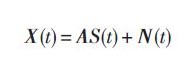
式中：X(t)为M × 1维的阵列输出向量;A为M × P维的阵列流型，它是辐射信号入射角α和β的函数;S(t)为P × 1维的入射信号向量;N(t)为M × 1维的噪声向量。由于信号与噪声相互独立，接收数据的协方差矩阵为：

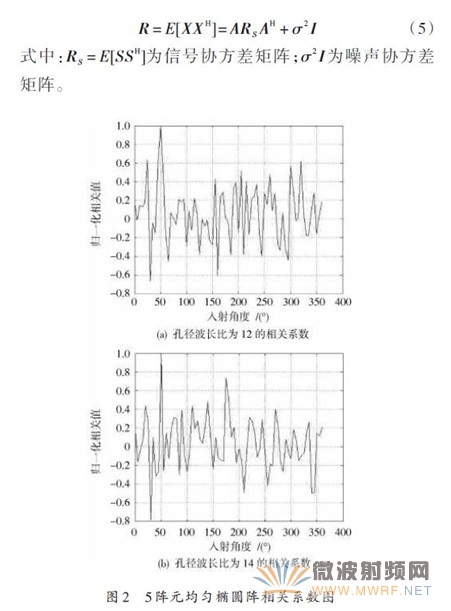
对R进行特征分解，P个大特征值对应的特征向量Us = [e1,e2 ,…，ep]张成信号子空间;M – P个小特征值对应的特征向量UN = [ep + 1,ep + 2 ,…，eM ]张成噪声子空间，两个子空间正交。在噪声子空间上投影为0的阵列流形所对应的方向就是信号的DOA,MUSIC算法通过搜索式(6)的极大值点来获得辐射信号的DOA:

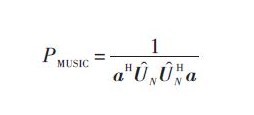
仿真分析2:

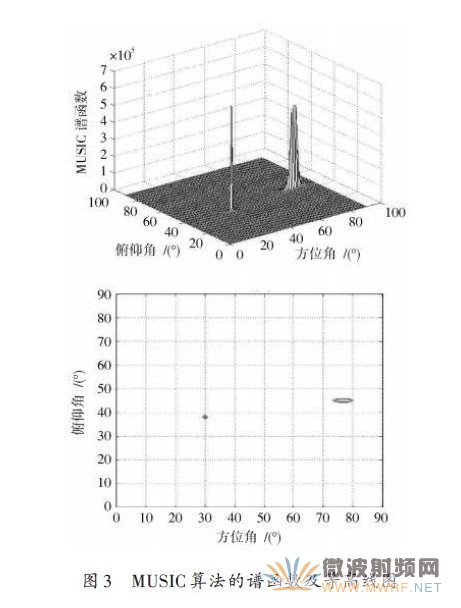
天线阵列采用均匀的5元椭圆阵，信噪比为20 dB,快拍数为1 000,取三个辐射信号(45°，75°)，(45°，78°)，(38°，30°)，仿真结果如图3所示。

仿真分析2:

天线阵列采用均匀的5元椭圆阵，信噪比为20 dB,快拍数为1 000,取三个辐射信号(45°，75°)，(45°，78°)，(38°，30°)，仿真结果如图3所示。

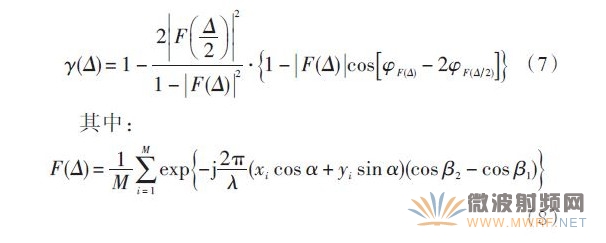
仿真分析3:

天线盘孔径对MUSIC算法分辨力的影响。天线阵列形式采用均匀的5 元椭圆阵，取两个辐射信号分别为(45°，75°)，(45°，78°)，即两个入射角间距为3°，依据式(7)对不同孔径与波长比(d λ)条件下的分辨能力进行仿真，如图4所示。

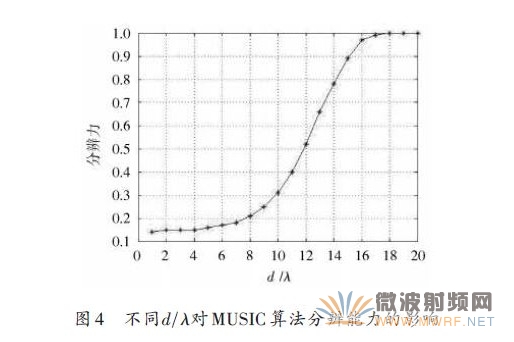
从图4可以看出，MUSIC算法分辨能力随天线盘孔径的增大而提高。故可以考虑通过增大天线盘孔径来提高MUSIC算法的分辨力，但天线盘的尺寸受限，不可以无限增大。鉴于四阶累积量的阵列具有扩展特性，利用它来增加