基于半周期积分算法的微小振动测量研究

作者 赵佳楠 张丕状 中北大学 信息探测与处理技术研究所(山西 太原 030051)

赵佳楠(1989-)，男，硕士生，研究方向：基于嵌入式的高速数据采集存储系统。

摘要：为了能够监测工厂机器的健康状况，并在机器出现故障征兆时尽早发现，本文设计了一套测量其关键部位振动状态的系统。该系统采用了基于FPGA的多通道大容量数据采集方案，并使用32片加速度传感器(型号为MPU6050)作为振动数据的采集模块。对保存下来的数据进行了频谱分析、去噪。当测量振动幅值时，加速度计的输出信号要经两次积分，引入的漂移将会随时间越来越大^[1]。为了减少漂移带来的影响，采用半周期积分算法来绘制机器各个关键部位的振动轨迹。通过绘制的各频率分量的振动波形，并与历史记录相比较，可以起到监测机器工作健康状况的作用。

引言

随着我国工业化程度越来越高，工厂中参与生产的现代化机器逐渐向大规模和高精度的特点发展，机器的各部分零件的衔接紧密程度也越来越高。随着机器工作时间的增长，各部分零件之间会产生一定的磨损。那么对于机器的健康状况的检测就成了一个减少损失很重要的方法。

现有的故障诊断方法整体上分成定性分析法和定量分析法两大类^[2]，其中定量分析法又分为数据驱动的方法和基于解析模型的方法^[3]。数据驱动的方法主要由五大类组成：信号处理、粗糙集、多元统计分析、信息融合及机器学习。本文是针对该方法中的信号处理分支所进行的算法研究。

常见的信号处理分析技术有以下几种：幅值域分析、时域分析、频域分析和时频域分析——小波分析方法^[4]。在幅值域分析方法中，人们是对采集到的振动点处的加速度信号进行处理，得到其相应的速度及幅值曲线。由加速度数据获得振动点的速度及幅值曲线需要经过两次积分，随着漂移的引入会使得对于积分结果的分析异常困难。

借助于机器振动的周期性以及相对于静止点的对称性等特点，本文采用了一种半周期积分算法。该算法能够很好地消除由于漂移带来的累积的积分误差，并将该误差限制于半个周期内。采用该算法获得的振动点的速度及幅值曲线能够很好地描述测试点的振动情况。

1 机器健康状况监测原理

1.1 振动点的振动信号来源分析

图1所示为实测的机器振动点的加速度频谱图。由图可知，测试点的振动来源不是单一的，是由连接该振动点的各个零件的振动共同叠加形成的。其叠加后的振动信号通过FFT变换产生的新的谐波分量可以一定程度上反应各个机器零件的振动情况。每个零件振动的中心频率一般是不变的^[5]，但是随着该零件的磨损程度逐渐加重，该零件振动的中心频率会发生一定的偏移，并会对该振动测试点的各振动频率分量产生明显的影响^[6]。

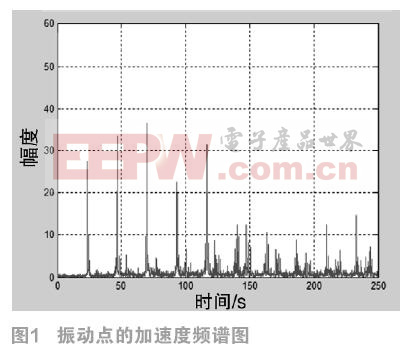
如果一个零件的磨损情况较为严重，其运转时会加重测试点的低频分量;如果一个零件发生断裂等严重的损坏，更是会直接影响到测试点的谐振频率分布。

1.2 振动信号的处理与分析

首先，被测振动点一般选择为各个零部件结合部，对于该监测点的监测才具有一定的参考价值。

其次，对于采集到的振动点的加速度数据，我们需要经过频谱分析，判断出哪些频率分量具有监测意义。频谱中存在不小的直流分量，这是需要我们去除掉的。直流分量的来源有以下两点：一是传感器本身的零漂，二则是重力加速度在测试点振动方向上的分量。滤掉直流分量后，将具有监测意义的谐振频率分量分离出来，并单独进行处理。

最后，将每一个单独分离出来的频率分量，通过半周期积分算法进行处理，绘制出该频率分量的幅值曲线。通过对该幅值曲线进行幅值域分析，获取其无量纲的幅值域参数，如裕度、峭度、波形、峰峰值、脉冲、斜度等，并与历史记录相比较，可以明显地显示出异常产生，以此来起到监测机器健康状况的作用。

2 硬件结构以及算法处理

本系统采用基于FPGA的大容量存储采集系统来监测机器的振动情况。其硬件结构为：主控芯片采用的是Xilinx公司的Spartan-3E系列的XC3S500E，同时使用了4片三星公司的NAND FLASH (K9NBG08U5A)芯片，该芯片每片有4GB的存储容量;加速度传感器采用的是MPU6050，其为6轴加速度陀螺仪传感器。主控芯片内部采用了MicroBlaze核进行数据处理，由于其内部数据以及地址总线都是32位，因此，在不采用模拟开关的情况下，最多可以同时对32路传感器进行数据存储。该系统采用USB口通过上位机对存储于FLASH中的数据进行读取，再在PC机上通过MATLAB进行数据处理以及轨迹恢复。

2.1 硬件设计

硬件的数据采集存储结构图如图2所示，使用的传感器模块大小为40mm×20mm。传感器模块采用柔性印制电路板，便于紧贴被测振动点表