基于半周期积分算法的微小振动测量研究

面。

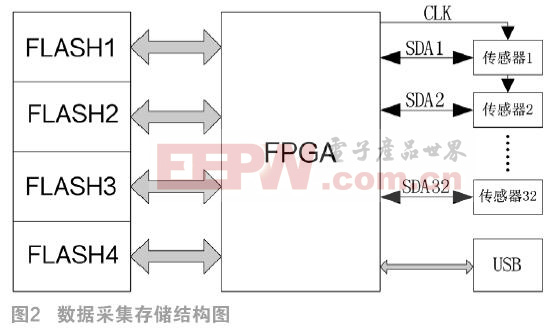
2.2 硬件程序

FPGA内部调用了MicroBlaze、中断等IP核，并且通过调用自己写的一个DMA程序生成的IP核来进行直接数据存储，加快了数据存储速率。

在SDK中，通过C语言写了FLASH、USB及I2C的一些驱动函数，通过上位机对该系统进行数据采集速率以及存储采集时间的配置，可以根据不同的监测条件选择合适的数据采集模式。

2.3 硬件相关参数

普通的单轴或者双轴加速度传感器都是垂直于振动方向的，无法进行测量。因此，选用了具有测量Z轴加速度功能的传感器MPU6050。

其加速度的测量范围选定为±16g，采样频率为1kHz，输出接口为I²C，内置AD的分辨率为16位。

2.4 加速度传感器的标定

对于单频率微小振动轨迹的绘制，需要克服以下难点：

1) 如何消除传感器本身的零漂;

2) 如何标定传感器本身的比例因子灵敏系数;

3) 如何消除数据的积分累积误差。

如表1，数据手册表明传感器Z轴零漂范围为±80mg，而比例因子灵敏系数的初始校准精度为±3 %。

为提高振动点的测量精度，在使用加速度计前需要对其各项参数进行标定。我们采用一种标定零漂和标度因子的六姿态校准方法，并建立标定方程来提高振动轨迹绘制精度。

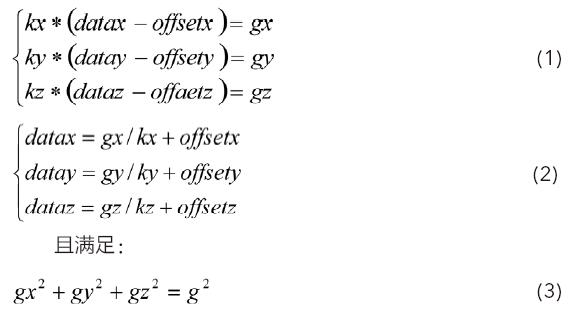
将式(1)、(2)、(3)整理，得到下面等式：

在对传感器进行标定后，我们不能对加速度直接进行二重积分，那样会将累积误差无限放大。

根据单频率振动的特点，我们分别对速度波形和振幅波形的绘制采用半周期积分法。这样就可以在消除累积误差的情况下，很好地绘制出振动轨迹。

2.5 半周期积分法^[8]

振动点在应力作用下，在平衡位置附近做往复运动。在振动点偏离平衡位置最大处，恰好是所测加速度值的一个极值点，也是速度值的零点;在振动点的平衡位置，则是加速度值的零点，是速度值的极值点。

根据以上特点，在对振动数据的加速度值进行处理时，我们采用半周期积分法，即从一个极值点积分到相邻的下一个极值点，然后积分值归零，再进行下一次积分。

例如，在由材料内部应力作用下而产生的振动情况中，对加速度从一个极大值点积分到下一个极小值点，对应的速度为从零点经过该速度的一个极大值点到下一个零点;对速度从一个极大值点积分到下一个极小值点，对应的振幅为从零点经过该振幅的一个极大值点到下一个零点。

3 结果检验与分析

3.1 单一频率振动轨迹绘制

为了验证系统的可靠性以及算法的优化程度，我们将对一个初始振动幅度为4mm的钟摆式振动进行轨迹绘制。

3.2 结果分析

图3是一个振动频率为19Hz、初始振幅为4mm的钟摆式振动加速度。

图4和图5分别是直接积分和采用半周期积分法得来的速度曲线。

图6和图7分别是直接积分和采用半周期积分法得来的振幅曲线。

由图4可以看出其有一个由累积积分误差引起的直流偏置分量^[9]，图6可以看出其由原始加速度经过二次积分对振幅带来的灾难性影响。

图7可以看出其最终描绘出的初始振幅第一个极大值点为3.453mm，第二个极大值点为4.206mm，该现象的产生来自于算法的精度误差。由于其初始值的最大幅度为4mm，其采样点之间的差值会比较大，导致最终积分结果有比较明显的差异。在振幅下降到1mm左右的时候，可以看出该算法精度误差^[10]影响就很小了。

4 结论

本文提出了一种处理振动加速度数据的新型算法——半周期积分法，该算法明显地降低了通过传统积分算法而产生的累积的积分误差，进而更加准确地描绘出了振动点的振幅波形。通过获取该振幅波形一系列无量纲的幅值域参数，可以准确地判断出机器的健康状况。

本文在仿真验证过程中，发现该算法对于振动点加速度数据采集的采样频率依赖性较高。对于振动幅值以及频率较大的振动点，要求采样频率也要相应的提高，以此就可以获得更加准确的振动波形。

参考文献：

[1]严普强,乔陶鹏.工程中的低频振动测量与其传感器[J].振动、测试与诊断,2002,04:3-9+75.

[2]周东华,胡艳艳.动态系统的故障诊断技术[J].自动化学报, 2009, 35(6): 748-758.

[3]杨永波. 基于机器学习的故障状态评价算法研究[D].辽宁大学,2013.

[4]孟小嵩.基于模式库的矿山设备健康诊断方法研究[D].中国矿业大学,2014.

[5]袁小宏,屈梁生.机器振动诊断中信号处理方法的研究[J].西安交通大学学报,2001,07:714-717+730.

[6]齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,01:86-92.

[7]张文瑞,张丕状,翟子雄.一种基于六姿态模型的加速度计校准方法研究[J].传感器与微系统,2016,03:37-39+48.

[8]SUN Yang, HUANG Jia dong, CHEN Da Zhuang. Novel Theory of Identifying Inrush Current Based on Half-cycle Sine Waveform[A]. Intelligent