利用Pspice通用测试电路实现关键参数的模拟（上）

在过去几年中，Spice模型得到了广泛的应用。一方面，IC制造商努力向客户提供精确的模型；另一方面，系统设计工程师日益要求采用更加精确的模型，这也促进了Spice宏模型的创新。许多IC公司都自诩拥有最棒的或者具备革命性新特性的模型，但他们往往未能向用户提供用于验证其宏模型精确度的测试电路。最常用的模型要算运算放大器宏模型，精确的运算放大器宏模型非常有用，但对于一般用户而言，使用这种模型会带来严重的问题。

大多数系统设计工程师在将运算放大器宏模型实现到一个综合性电路中之前，都会对其进行测试。然而不幸的是，面对错误的模拟结果，系统设计师会直接向IC制造商的应用工程师抱怨，他们开发的模型毫无用处，而当IC制造商的应用工程师试图了解模型运行的具体情况时，得到的回答却是“哦，在采用贵方竞争对手提供的另一种模型时，我的电路就能得出正确的结果。”

事实是，每一种模型都不尽相同，有的可能不能支持某个特定设置。因此，我认为，最好的办法不是弄清楚各个运算放大器宏模型存在的缺陷，而是提供一套能够支持任何运算放大器宏模型的电路，也就是提供一套面向各种运算放大器宏模型的通用测试电路。

宏模型的区别主要在于其测试参数的复杂程度，模型的任务是模拟运算放大器认为与应用相关的参数。例如，对于轨对轨输出运算放大器，用户需要测试并验证输出饱和电压与负载电流的关系。同样地，低噪声放大器应该有一个至少能模拟电压噪声的模型。除了它们之间的差异，各种放大器宏模型也可以模拟一些相同的参数。在执行模拟时，往往是从下面这些最值得关注的参数开始。

开环增益和相位容限

系统设计师在评估其放大器宏模型的性能时，一般首先会测试其开环增益与频率的关系。这个测试非常重要，因为设计师可以利用一个简单的小电路，了解模型的DC增益、-3dB频率、交叉频率(如果是电压反馈放大器，则为增益带宽积)和相位容限。

图1a所示为测试电路，RC网络确保在适当的DC电压下产生输出偏流。在较高频率下，电容会将倒相输入短路接地，使运算放大器处于开环状态。这个电路采用了一个较大的电容，以尽快降低增益(f=2πRC)。因此，即便被测运算放大器的主极点频率极低，用户也可以模拟并实现平稳的变化，滚降速率为20dB/十倍频程。

在测试开环增益和相位时，用户选择的频率范围应当高于放大器的单位增益带宽。在使用轨对轨输出模型时，用户必须向测试电路施加数据表中规定的负载，否则模拟结果可能发生错误，尤其是DC增益(AOL=gmRL)。

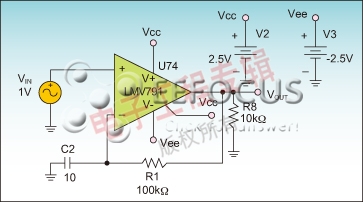
图1a：开环增益和相位测试电路

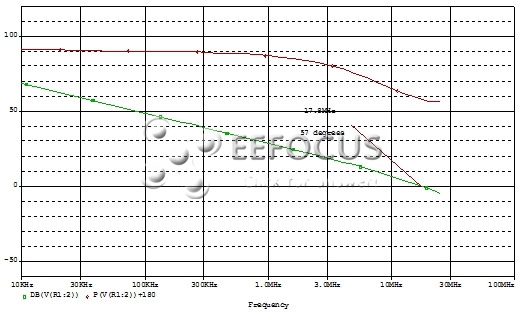
图1b：开环增益和相位模拟

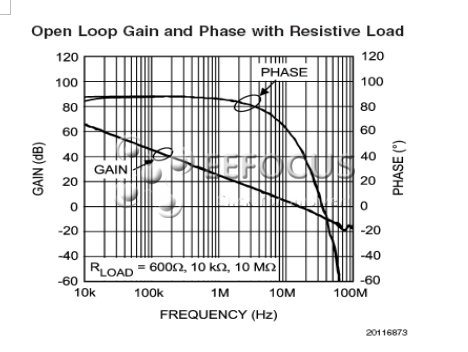
图1c：开环增益和相位测试结果

压摆率

压摆率是一个放大器速度参数，所有模型都应当能够模拟这个参数。压摆率等于尾电流与补偿电容的比值。根据所用的宏模型，用户可以将决定压摆率的电容置于输入端口或者一个单独的网络中。

我们已经知道Idt=Cdv这个关系，因此，可以直接利用图2a所示电路，根据输出值计算出压摆率。用户只需要利用插入命令，在探针屏幕上显示的输出电压值之前，键入字母“d”。

在执行压摆率模拟时，请确保将模型设置为瞬态，使输入信号具备足够快的上升时间和下降时间，不会对压摆率造成限制。同时，用户必须根据运算放大器的速率，选择相应的输入信号频率。输入信号频率过高会导致收敛问题。

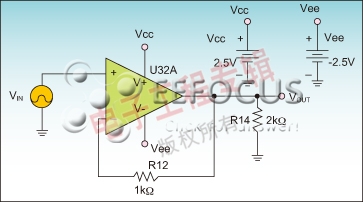
图2a：压摆率测试电路

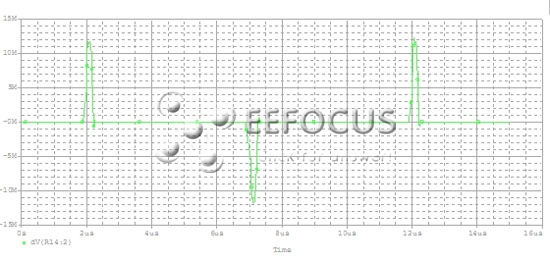
图2b：压摆率模拟

CMRR和PSRR

虽然有的模型不能模拟这两个参数，但这两个参数很重要。通常，共模抑制比(CMRR)和电源抑制比(PSRR)模拟电路由一个简单的RC网络、一个电阻分压器和一个电压控制电源构成，用户可以在模型中轻松实现这两个参数。

在非倒相配置中，由于调制器的存在，CMRR变得尤为重要。此外，如果某个应用的电源容易受到干扰，那么PSRR就非常重要。

借助图3和图4所示测试电路，用户可以模拟这两个参数。如果正确地模拟了这两个参数，那么极点和零点位置应当与数据表中的曲线图相一致。

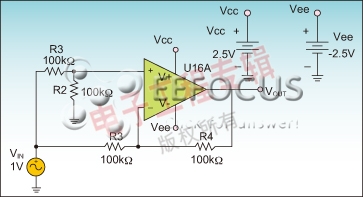
图3a：CMRR测试电路

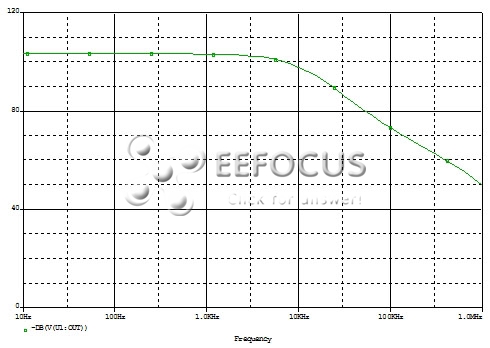
图3b：CMRR响应与信号频率关系模拟

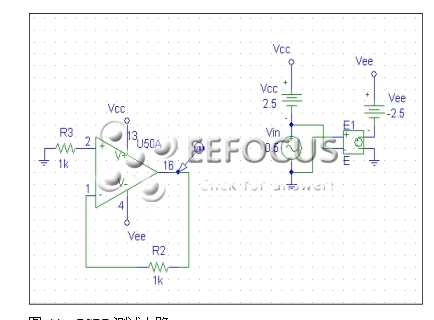
图4a：PSRR测试电路

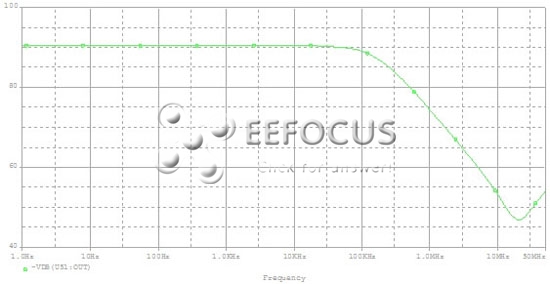
图4b：PSRR响应与信号频率关系模拟

输出阻抗

通常，数据表中不包含这个参数，但有时候必须测试这个参数。如果正确地实现了模拟，用户可以通过输出阻抗更加精确地计算出放大器在驱动电容性负载时的稳定时间。

在设计旨在实现稳定性的补偿方案时，也需要根据输出阻抗计算出适当的元件值。借助这个图5的测试电路，用户可以在频域内使用3种不同的增益值，模拟相应的输出阻抗。输出电压与1A电源电流的比值即为输出