有源钳位正激变换器的功率损耗分析
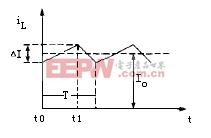
有源钳位正激变换器的电路参数 在工作模态1中,输出电感电压为: 电流纹波的峰峰值 是: 图7是输出电感电流iL的波形图,由图可得iL表达式 图 7 输出电流iL的波形 fig7.The waveform of output current iL 此模态中,变压器二次侧电流 ,则二次绕组的电阻产生的功率损耗为 , 把式(3),式(4)代入,则可得 显然,如果L值很大,则 ,那么括号中前面一项可以忽略,PC2可简单表示为等式(5) 假设漏感 远小于励磁电感 ,可以忽略。初级侧电流i1用表示如下: 则模态1下的功率损耗P1为式(6), 上式RTI 为初级侧总电阻,用下式表示: 开关模态2,整个钳位电路的总电阻为: 式中ESR为钳位电容的等效串联电阻。模态2一次侧的回路电压方程为: 很明显,如果钳位电路的电阻RT2非常小,而励磁电感Lm很大,使得 等式(7)可简化为: 由上分析可得模态2的功率损耗为: 其中 开关模态3,因为死区时间(t1 ~t2 )足够大,所以i3(t-t2) 初始值i3 (t2)为零。此模态的电压回路方程为: 式中 为此模态回路的总电阻。 由上式可得: 此模态功率损耗P4为: 此模态钳位电路的总电阻RT4为: 根据以上讨论,可得一个开关周期变换器的功率总损耗是: 已有许多文献指出,此变换器稳态工作时模态1的损耗远大于其他开关模态的损耗,为简化分析,一般用P1代替一个开关周期的功率总损耗,则模态1的损耗P1重新表示为: 式(11)又可写为下面式(12)的形式 现P1对Lm求微分,得式(13) 现令式(13)等于零可求出Lm的值。P1对 对图1所给的实验电路,设定匝数比为n=3,输入电压Vi=48V, Io=10A, Vo=3.3V, t1=1.5×10-6s,T=5×10-6s,R=0.3Ω,可以得到功率损耗与励磁电感的关系曲线如图8所示。 以上讨论的是有源钳位正激变换器稳态时的功率损耗,是忽略了变压器漏感,不考虑主开关和钳位开关寄生电容的简化分析结果。在实际的电路中,变压器的漏感和主开关的等效寄生输出电容作用,使得励磁电流可能会产生直流偏置的问题[4],可以通过减少漏感或调节励磁电感的大小来使得励磁电流的直流偏置最小。另外,励磁电感的大小也决定了主开关管零电压软开通是否能够实现。因为当变压器励磁电感Lm减少,励磁电流足够大时,励磁电流除了提供负载电流外,剩余部分可用来帮助主开关和钳位开关的寄生电容充放电,使主开关漏源极电压有可能谐振到零,从而实现主功率开关管的零电压软开通,进而减少开通损耗。但又要考虑到软开通的代价是变压器的励磁电流和开关管导通电流峰峰值大幅增加,开关管及变压器电流应力和通态损耗明显加大。所以在变压器设计时,励磁电感的选择很关键。在设计时要综合考虑以上因素,在坚持效率优先的前提下,尽量使设计达到最优。 5.结语 本文分析和讨论了有源钳位正激变换器稳态工作时的功率损耗,得出它与励磁电感之间的关系。表明在一定的磁链关系下,存在着一个最优的励磁电感,使得变换器的功率损耗最小,效率最优。
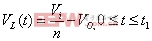
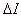
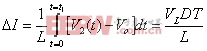 (3)
(3)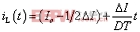 (4)
(4)
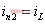
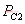
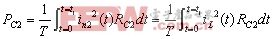
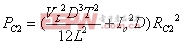
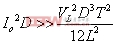
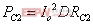
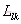

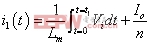 (5)
(5) (6)
(6)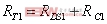
根据(5)式,可以看出随着Lm的减小,i1(t)在Io/n的基础上增大,由于S1存在导通电阻,所以功率损耗增大。另一方面,由(1)式、(2)式可得RC1,RC2亦会增大,所以总的损耗P1增加。输出电流越大,损耗效果越明显。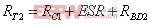
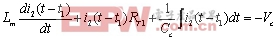
由上式可求得i2(t-t1):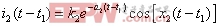
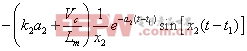 (7)
(7)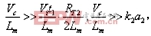
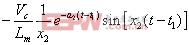
 (8)
(8)
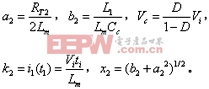

同样由上式可求得i3(t):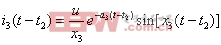
模态3的功率损耗P3 为:

开关模态4时的回路方程为: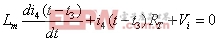
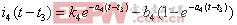
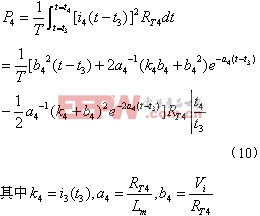
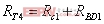
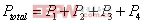
4.最优电感的确定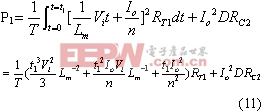
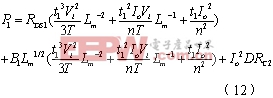

Lm求二次微分得式(14):
根据数学理论可知,如果上面求得的Lm值使得式(14)大于零,就存在最小的功率损耗。也就是说可以根据式(13),式(14)找到最优的Lm使变换器的功率损耗最小。 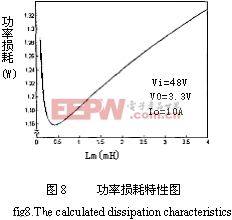
由上图可看出,不同的励磁电感值对应不同的损耗值,由图所得到的最小功率损耗值及其对应的励磁电感值与根据式(12),式(13)精确计算得到的最小损耗值P1 =1.1584W,Lm =429micro;H基本吻合。
对于有源钳位正激变换器。本文所提出的有关励磁电感的观点和设计准则,在设计一个确定匝数比的隔离变压器时十分有用。
- 具扩展频谱频率调制的低EMI DC/DC稳压器电路(12-24)
- EMI/EMC设计讲座(三)传导式EMI的测量技术(07-20)
- 扩展射频频谱分析仪可用范围的高阻抗FET探头(07-14)
- 开关电源基于补偿原理的无源共模干扰抑制技术(08-27)
- 开关电源的无源共模干扰抑制技术(11-12)
- 省电设计使DDS更适合便携应用(12-19)
