松耦合全桥谐振变换器的传输特性分析研究
摘要:本文对基于非接触式感应电能传输技术的全桥谐振变换器的传输特性进行了研究。首先,本文以原副边均采用串联补偿为例进行分析,通过matlab仿真计算,得出了这种情况下补偿电容的变化、负载的变化对原边谐振频率和传输特性的影响。其次,分析了发生频率分叉现象时工作频率该如何选择,并利用反映阻抗的概念分析了变换器的功率传输能力。最后基于实验样机对文中分析与结论进行了实验验证。 叙词:补偿;传输特性;谐振频率;频率分叉现象 Abstract:In this paper, the transfer characteristic of loosely coupled inductive power transfer full-bridge resonant converter is studied. Firstlywe obtain the conclusion that how the compensation capacitor and load influence on resonant frequency and transfer characteristic, making use of MATLAB, taking the situation that primary and secondary compensation is series for example. Secondly, how to choose the switching frequency when bifurcation phenomena occurs is analyzed, besides, the transfer capability is also analyzed using the conception of reflection impedance. Finally, experimental results from a prototype of full-bridge converter are given, which verify the correctness of analysis and conclusion in the paper. Keyword:compensation; transfer characteristic ; resonant frequency; bifurcation phenomena
1前言:
在非接触式感应电能传输系统中,能量发射装置和能量接受装置是通过一个松耦合的变压器来实现的。变压器原边和副边之间有一个较大的气隙,变压器的耦合系数很低,漏感很大,一般情况下,漏感和励磁电感处在同一个数量级。采用互感模型分析可分离变压器,利用互感来描述初、次极的耦合能力,这种模型能很好的指导非接触式能量传输系统的设计。
由于漏感较大,它不仅影响能量传输的功率和效率,而且大幅度加大功率器件的电压和电流应力。图1为初级次级都不加补偿的松耦合谐振变换器,流过变压器的电流近似线性变化。为了得到较高的功率传输比,降低由漏感所引起的开关管的高电压应力,减小变压器
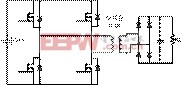
图1原副边都不加补偿的松耦合谐振变换器
对周围环境的电磁辐射,必须在松耦合变压器原副边加入适当的补偿电路,这样,不仅能使电路中的电流尽量正弦化,减小了辐射,而且也有效利用了电路中的寄生参数,减小了寄生参数对电路的影响[1]。
近年来,针对松耦合变换器的原副边的具体补偿问题在国内外已经展开了广泛深入的研究,文献[2]对原边串联副边并联补偿的频率分叉现象作了详细研究,但是到目前为止还没有专门的文献对补偿后的传输特性,即输出电压随着频率、补偿电容和负载电阻的变化给予深入的研究,本文就这方面给予比较详细的研究。
本文以基于松耦合变压器的全桥谐振变换器为例,用原边串联补偿的拓扑来降低功率器件的电压应力,重点研究了副边是串联补偿的传输特性,并对原边副边为串联补偿时的频率分叉现象也进行了详细的分析。最后分别对变负载和改变补偿电容进行了试验对比分析,从而验证了文中理论分析的正确性。
2基于松耦合变压器的全桥谐振变换器的理论分析
在仿真计算中,变压器的参数不变,取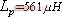 ,
,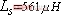 ,
,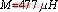 ,只讨论负载电阻和补偿电容变化对输出的影响。
,只讨论负载电阻和补偿电容变化对输出的影响。
对于图2所示全桥谐振变换器,在双极性控制方式下,如果只考虑基波的作用,忽略高次谐波,开关网络的桥臂中点电压可以用正弦
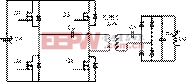
图2 原副边均为串联补偿的谐振变换器
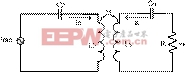
图3等效电路
电压源等效。![]() 是整流桥输出电压,与等效交流电的关系为,
是整流桥输出电压,与等效交流电的关系为,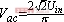 。并根据正弦等效原理,变换器副边整流电路与交流电阻的关系为
。并根据正弦等效原理,变换器副边整流电路与交流电阻的关系为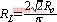 。输出整流电压
。输出整流电压![]() 与交流等效电阻电压关系为
与交流等效电阻电压关系为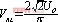 。在不考虑原副边损耗的情况下可得到如图3的等效电路[3],对图3稳态电路进行分析。
。在不考虑原副边损耗的情况下可得到如图3的等效电路[3],对图3稳态电路进行分析。
对原副边分别列写电路方程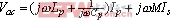 (1)
(1)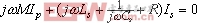 (2)又
(2)又 ,
,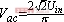 ,
,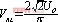
解以上方程可得
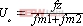 (3)
(3)
其中,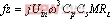

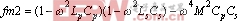
副边反应到原边的反映阻抗为 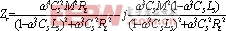 (4)
(4)
整个电路的总阻抗
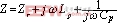 (5)
(5)
总阻抗![]() 的实部
的实部
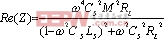 (6) 总阻抗
(6) 总阻抗![]() 的虚部
的虚部 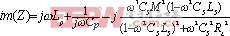 (7)通分后可得令虚部为零可得
(7)通分后可得令虚部为零可得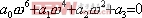 (8)其中,
(8)其中,
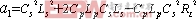
 ,
,![]()
一般情况下![]() ,故上式为一元六次方程,可能有多个实数解,若用数值分析的方法求方程的解将十分复杂,本文利用matlab计算总阻抗
,故上式为一元六次方程,可能有多个实数解,若用数值分析的方法求方程的解将十分复杂,本文利用matlab计算总阻抗![]() 阻抗角
阻抗角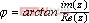 为零的
为零的![]() 值即为虚部为零时的
值即为虚部为零时的![]() 值。图4、图5分别为
值。图4、图5分别为![]() 或
或![]() 不变时,阻抗角与补偿电容
不变时,阻抗角与补偿电容![]() 和
和![]() 的关系图。由图4可见,随着副边补偿
的关系图。由图4可见,随着副边补偿
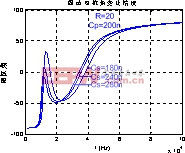
图4 Cs不同时阻抗角变化情况
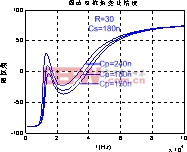
图5 Cp不同时阻抗角变化情况
电容![]() 的减小,阻抗角为零的点由一个变为三个。由图5看出,随着原边补偿电容的增加,阻抗角为零的点也由一个变为三个。这说明对于某些补偿电容值,电路有多个谐振点,这种现象称之为频率分叉现象。频率较低的称之为低谐振点,频率较高的称之为高谐振点。下面讨论的是如果发生频率分叉现象,在各个谐振点的功率传输情况。
的减小,阻抗角为零的点由一个变为三个。由图5看出,随着原边补偿电容的增加,阻抗角为零的点也由一个变为三个。这说明对于某些补偿电容值,电路有多个谐振点,这种现象称之为频率分叉现象。频率较低的称之为低谐振点,频率较高的称之为高谐振点。下面讨论的是如果发生频率分叉现象,在各个谐振点的功率传输情况。
- 存储器特性分析和预测应用处理器性能及功耗(01-17)
- 在EMI滤波器设计中的干扰特性和阻抗特性讲解(01-12)
- 基于EMI滤波器设计中的干扰特性和阻抗特性的研究(01-12)
- 资深工程师电磁兼容设计精髓总结:高频状态电路特性(01-11)
- 光伏阵列故障诊断方法综述(05-06)
- 推挽升压型耦合电能传输系统DC/DC变换器研究(03-20)
