松耦合全桥谐振变换器的传输特性分析研究
3传输特性分析
对(3)式进行matlab计算仿真,仿真参数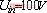 ,
,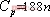 ,
,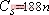 ,负载分别为
,负载分别为![]() 、
、![]() 、
、![]() 。
。
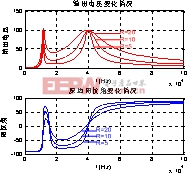
图6负载不同时阻抗角和输出电压变化图
图6为负载不同时阻抗角和输出电压变化的matlab仿真图,由图可见,在负载不变的情况下,随着频率的变化,输出电压有两个极值点。输出电压的极值是在高谐振频率和低谐振频率点取得的,在中间的谐振点,输出电压较低,相应的输出功率就较小。该规律可以用反应阻抗的概念来解释。由式(6),的实部就是就是副边阻抗反映到原边阻抗的实部,所取得的功率即是副边负载所取得的功率[2]。
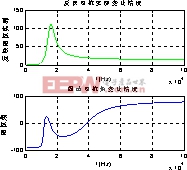
图7反映阻抗实部和阻抗角变化图
图7为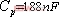 ,
,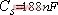 ,负载为
,负载为![]() 原边阻抗角和副边反映阻抗实部随着频率
原边阻抗角和副边反映阻抗实部随着频率![]() 变化图。由图可见,在高谐振点和低谐振点,反映阻抗实部比较小,相应的得到了较大的输出功率,而在中间的谐振点,反映阻抗实部达到了最大值,故输出功率较小。
变化图。由图可见,在高谐振点和低谐振点,反映阻抗实部比较小,相应的得到了较大的输出功率,而在中间的谐振点,反映阻抗实部达到了最大值,故输出功率较小。
由图6还可以得出,当原副边补偿电容不变,负载电阻在一定范围内变化时,谐振频率基本不变。
在上面的计算仿真中,没有考虑电路的损耗。图8为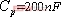 ,
,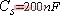 ,负载分别为
,负载分别为![]() 、
、![]() 、
、![]() ,考虑原副边损
,考虑原副边损
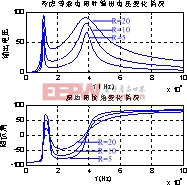
图8考虑损耗时输出
耗时的输出电压变化情况。在考虑原副边损耗时,输出电压有了较大幅度的变化。负载电阻值越大,输出电压越高。
4发生频率分叉现象时工作频率的选取
图9和图10分别是和改变时的阻抗角和输出电压随开关频率变化图。综合图6、9、10,可以看出,虽然低谐振点和高谐振点都可能得到较大的功率输出,但在低谐振点附近,输出电压随着频率变化的曲线非常陡,说明输出电压对频率的变化非常敏感。频率稍微偏离低谐振点,输出电压就会变化很多。
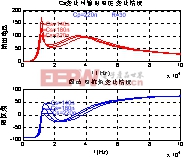
图9 Cp不同时电压和阻抗角变化图
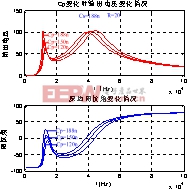
图10 Cs不同时的电压和阻抗角变化图
在低谐振频率点附近的最高输出电压还随着补偿电容![]() 和
和![]() 的变化而变化,而且变化的幅度很大,说明了输出功率也有大幅度的变化。而高谐振点附近,输出的最高电压变化幅度很小,可以得到比较稳定的功率输出。
的变化而变化,而且变化的幅度很大,说明了输出功率也有大幅度的变化。而高谐振点附近,输出的最高电压变化幅度很小,可以得到比较稳定的功率输出。
此外,低谐振点的频率![]() 较小,如果需副边输出相同的功率,工作于低谐振点时的开关器件的电流应力比高谐振点大,这在大功率应用中,导通损耗将增加很多。
较小,如果需副边输出相同的功率,工作于低谐振点时的开关器件的电流应力比高谐振点大,这在大功率应用中,导通损耗将增加很多。
综上所述,在本文的实验中,所选取的工作频率在高谐振点附近。
当原边补偿电容或者副边补偿电容增加时,由图9和图10可知电路的谐振频率将减小。在实际应用中,如果采用频率跟踪的控制方法,只要选取合适的补偿电容,使电路的高谐振点频率与其他两个谐振点频率相差比较大,远离其他两个谐振点,就能使频率跟踪电路易于工作在高谐振点附近,得到较大的功率输出。当原副边为串联补偿的松耦合变换器补偿电容在一定范围内变化时,如果采用频率跟踪的控制方式,就能使负载得到最大功率的输出。这时,在副边功率相同的情况下,原边所需的视在功率最小,系统效率最高。
5实验验证
为了验证文中理论分析,针对于原副边边均为串联补偿的变换器,设计制作了一台松耦合全桥变换器的原理样机。松耦合变压器采用UF100B的U型磁芯,原副边绕组匝数为20匝,每个磁芯的两个芯柱各绕10匝,以尽量提高耦合系数,气隙![]() 。参数:
。参数: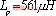 ,
,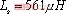 ,
,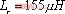 ,
,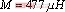 , 图8为
, 图8为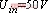 ,
,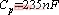 ,
,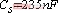 负载分别为
负载分别为![]() 、
、![]() 时的输出与频率之间的关系图。由图11可见,在开关频率为
时的输出与频率之间的关系图。由图11可见,在开关频率为![]() 的时候,两种负载下输出电压都达到最大值,说明此时电路基本处于谐振频率状态。这也验证了负载在一定范围内变化时谐振频率基本不变。而且,输出电压
的时候,两种负载下输出电压都达到最大值,说明此时电路基本处于谐振频率状态。这也验证了负载在一定范围内变化时谐振频率基本不变。而且,输出电压
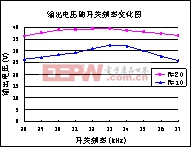
图11输出与频率的关系
随着开关频率的变化很小,这也和前面的分析是一致的。由于实际电路存在损耗,所以负载电阻越大在谐振点输出电压越高,这和图9仿真计算的结果是一致的。
图12和图13是补偿电容不同时,同一负载在不同的谐振频率处的输入输出关系图,其中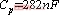 ,
,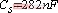 ,
,![]() 分别为
分别为![]() 、
、![]() 时,谐振频率为
时,谐振频率为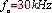 ;
;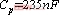 ,
,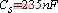 ,
,![]() 分别为
分别为![]() 、
、![]() 时谐振频率为
时谐振频率为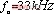 。从图12和图13可以看出,虽然补偿电容不同,但在各自的高谐振点附近得到的输出电压是相差不大。因此,原副边的补偿电容在一定范围内变化时,采用频率跟踪的方式跟踪系统的谐振频率,使系统工作在高谐振点,负载得到的功率是很接近的,这和前面分析是一致。
。从图12和图13可以看出,虽然补偿电容不同,但在各自的高谐振点附近得到的输出电压是相差不大。因此,原副边的补偿电容在一定范围内变化时,采用频率跟踪的方式跟踪系统的谐振频率,使系统工作在高谐振点,负载得到的功率是很接近的,这和前面分析是一致。
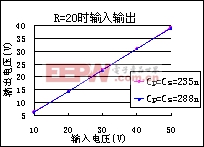
图12 R=20补偿电容不同时的输入输出
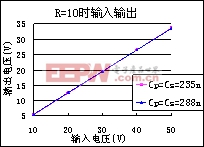
图13 R=10补偿电容不同时的输入输出
图14为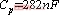 ,
,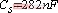 ,
,![]() ,开关频率
,开关频率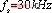 时驱动、桥臂中点电压、输入电流和原边补偿电容电压的波形,考虑
时驱动、桥臂中点电压、输入电流和原边补偿电容电压的波形,考虑

图14 f=30kHz
到电流是用LEM检测的,有的延时,可见电压和电流基本同相位,系统处于谐振状态。图15是时桥臂中点电压和电流波形,此时开关频率小于谐振频率,电压滞后于电流。图16是时桥臂中点电压和电流波形,此时开关频率大于谐振频率,电压超前于电流。


图15 f=27.3kHz 图16 f=37.7kHz
6结论
原边串联副边串联补偿的松耦合谐振变换器有以
- 存储器特性分析和预测应用处理器性能及功耗(01-17)
- 在EMI滤波器设计中的干扰特性和阻抗特性讲解(01-12)
- 基于EMI滤波器设计中的干扰特性和阻抗特性的研究(01-12)
- 资深工程师电磁兼容设计精髓总结:高频状态电路特性(01-11)
- 光伏阵列故障诊断方法综述(05-06)
- 推挽升压型耦合电能传输系统DC/DC变换器研究(03-20)
