脉冲变压器的磁学（下）

25所示。U2和负载两端的电压非常地接近。LL的阻抗和频率f成正比。CD的阻抗和频率f成反比。两者引起的效应是：当f∞则U20，如图26所示。

高频响应主要是漏电感和分布电容起作用。当这些参数值很低时，就能得到比较好的高频响应。

7.3运行的频率响应

在理想的情况下，变压器的运行区间在它频率范围之内，变压器就相当于一个理想元件。,如果RSOURCERLOAD则U2=U1

在实际等效电路参数下，会使输出电压减小一些，这种衰减通常用插入损耗（dB）来表示。

插入损耗（dB）=10log（U2/U1）

综合7.1～7.3节可得到图27所示的频响曲线。

8时域响应特性

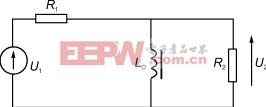
图32脉冲平顶响应

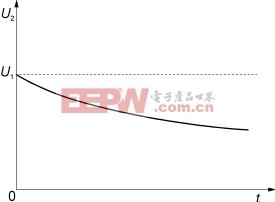
图31脉冲平顶响应的等效电路

图33下降沿等效电路

图34下降沿的响应

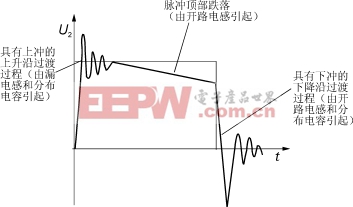
图35变压器的脉冲响应

本节将给出一个简单脉冲变压器的时域响应特性的简单说明。完整的含有许多方程分析起来相当复杂，为了简化分析，在本节中做下列假设：

（1）绕组电阻和源电阻及负载电阻相比是可以忽略的；

（2）漏电感可以集中在一项里；

（3）磁芯损耗电流和负载电流相比可以忽略；

（4）绕组之间的电容效应可以忽略。

这些假设对大多数实际情况来说是可行的，不会改变所获得基本特性的数据。在此假设下，可把图22的等效电路简化成如图28所示。

8.1脉冲上升沿响应

等效电路如图29所示。对于瞬间变化的输入电压而言，加在它上面的开路电感的阻抗是趋向无限大，可以忽略。假设源电阻R1也可忽略。

在此假设下，计算节点X的电流，并通过对它的方程求导数就能得到二次微分方程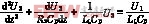：这个方程的解是：

U2=U1(1＋Ae－αt＋Be－βt)(23)

图27变压器的频率响应

图26高频响应

由这个方程得出的波形如图30所示。超调量和波形的上升时间取决于R2，L2和CD的值。

8.2脉冲平顶响应

在脉冲上升沿的过渡过程结束后，就进入理想脉冲的第二阶段，脉冲平顶响应部分。其等效电路如图31所示。漏电感远小于开路电感，可以忽略。在脉冲峰值持续期间分布电容上电压的变化率是很小的，通过它的电流比负载电流很小，所以它也可以忽略。

在此假设下，我们再一次计算电流，并通过它的方程对时间求导数，就能得到一次微分方程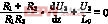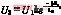：此方程的解是：

负载电压离开初始值后按指数规律下降，如图32所示。下降速率和开路电感成反比，即开路电感L0数值愈大，在脉冲持续期间，负载电压偏离初始值就愈小。

8.3脉冲下降沿响应

等效电路如图33所示。漏感通常比开路电感小，可以忽略。

在此假设下，先计算电流，然后再通过它对时间求导数，可以得到二次微分方程：此方程的解是：U2=U1(Aeαt＋Beβt)

波形的形状取决于开路电感和CD的数值。

如果磁芯的励磁电流可以忽略，则其衰减的波形，一般来说是指数衰减的阻尼正弦振荡，如图34所示。

如果忽略了过大的励磁电流，随着磁场的衰减，将会发生一个再生电动势，引起一个很大的下冲。

综合8.1和8.3节的结果，就能得到完整的脉冲响应曲线，如图35所示。为了清楚起见，图中的过渡过程和下降的峰值是被放大了的，在一个好的变压器设计中，这些将是很不显著的。