基于空间矢量调制的三相矩阵式变换器
0 引言
随着可控交流电气传动的发展,PWM变频器的应用为自动化和节能赢得了可观的效益,同时也带来了谐波污染、低功率因数、直流滤波电容寿命有限等负面影响。而“绿色”变频器应具备输入和输出电流都是正弦波;输入功率因数可控,带任何负载都能使功率因数为1.0;可获得工频上下可控的输出频率等品质。目前的三电平双PWM交—直—交变频器、多逆变单元串联的中压变频器虽都可达到或接近这些要求,但这些装置非常笨重。矩阵式变换器与其相比具有下述非常明显的优势:
——输入功率因数正负可调,输出电压频率连续调节,功率可双向流动;
——无直流母线环节,传递能量密度高;
——输入波形好,无低次谐波,波形失真度小;
——体积小,结构紧凑。
正因为矩阵式变换器具有如此明显的优势,近年来它已成为电力电子研究的热点之一。
1 矩阵式变换器的结构
3φ-3φ矩阵式变换器是一种强迫换相的交—交变换器,它由9个可控的双向开关,利用PWM控制将交流供电电源直接变换成负载所需的变压变频电源。其结构如图1所示。输入侧的L-C滤波器可有效减少输入电流的开关频率谐波。
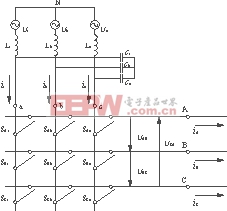
图1 矩阵式变换器的原理结构图
Fig 1 principle configuration of matrix converter
采用空间矢量调制时,矩阵式变换器认为是两个部分的串联组合。第一部分是AC/DC电压源整流,第二部分是DC/AC电压源逆变。图2是矩阵式变换器的等效交—直—交结构。
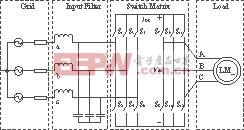
图2 矩阵式变换器的等效交—直—交结构
Fig 2 the equivalent AC/DC/AC structure of matrix converter
2 空间矢量调制(SVM)
能满足输入电压不被短路、输出电流不突然开路的矩阵式变换器开关组合共有27种,但有6种在等效交—直—交变换中找不到对应的开关组合,这6种是三个输出相分别连到三个输入相的开关组合。可用的21种开关组合如表1所列,表1中的“1”表示开关导通,“0”表示开关关断,第一组1P—9N三个输出相分别与两个输入相相连,剩下的第二组三个输出相仅与一个输入相相连而被短路。对于等效交—直—交变换的每一个合法的开关状态,矩阵式变换器有唯一的开关状态与之相对应。
三相开关动作所能形成的定子电压空间矢量有8种,即6种有效矢量U1~U6,依次表示U1(100)、U2(110)、U3(010)、U4(011)、U5(001)、U6(101),2种零矢量U7及U8,表示为U7(000)和U8(111),它们的空间位置和相互关系如图3所示。括号中的数字,第一位表示A相,第二位表示B相,第三位表示C相,当某一相的上桥臂开关导通时记为1,下桥臂开关导通时记为0。利用这些电压空间矢量的线性组合,可以获得更多的与U1~U8相位不同的新的电压空间矢量,最终构成一组等幅不同相位的电压空间矢量。
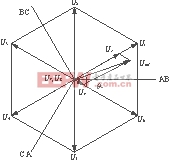
图3 电压空间矢量图
Fig 3 the inverter voltage vector
如图3用U1、U6和零矢量来合成新的矢量,各矢量的作用时间可用开关周期Ts中的占空比来表示。
U1矢量的占空比(作用时间)为
Dα=tα/Ts=musin(60°-θv)(1)
U6矢量的占空比(作用时间)为
Dβ=tβ/Ts=musinθv(2)
零矢量的占空比(作用时间)为
Dou=tou/Ts=1-Dα-Dβ(3)
式中:mu为电压调制系数,0=mu=![]()
![]() =1。同理对于虚拟整流器部分也可采用复空间表达方式定义输入相电流矢量,获得输入电流空间矢量调制的方案。
=1。同理对于虚拟整流器部分也可采用复空间表达方式定义输入相电流矢量,获得输入电流空间矢量调制的方案。
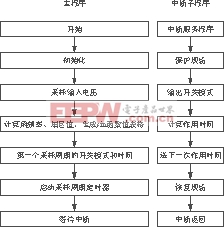
图4 电流空间矢量图
Fig 4 the rectifier current vector
表1 矩阵式变换器有效开关组合表及与等效交—直—交变换器对应关系
Tab 1 Valid switch combinations of a matrix converter and thestationary vectors
| 21矢量 开关组合 | 开关状态 | 输出电压 | 输入电流 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SAaSAbSAc | SBaSBbSBc | SCaSCbSCc | UAB | UBC | UCA | Ia | Ib | Ic | |
| 1P | 100 | 010 | 010 | Uab | 0 | -Uab | IA | -IA | 0 |
| 1N | 010 | 100 | 100 | -Uab | 0 | Uab | -IA | IA | 0 |
| 2P | 010 | 001 | 001 | Ubc | 0 | -Ubc | 0 | IA | -IA |
| 2N | 001 | 010 | 010 | -Ubc | 0 | Ubc | 0 | -IA | -IA |
| 3P | 001 | 100 | 100 | Uca | 0 | -Uca | -IA | 0 | IA |
| 3N | 100 | 001 | 001 | -Uca | 0 | Uca | IA | 0 | -IA |
| 4P | 010 | 100 | 010 | -Uab | Uab | 0 | IB | -IB | 0 |
| 4N | 100 | 010 | 100 | Uab | -Uab | 0 | -IB | IB | 0 |
| 5P | 001 | 010 | 001 | -Ubc | Ubc | 0 | IB | IA | IC |
| 5N | 010 | 001 | 010 | Ubc | -Ubc | 0 | 0 | -IB | IB |
| 6P | 100 | 001 | 100 | -Uca | Uca | 0 | IB | IC | IA |
| 6N | 001 | 100 | 001 | Uca | -Uca | 0 | IB | 0 | -IB |
| 7P | 010 | 010 | 100 | 0 | -Uab | Uab | IA | -IA | 0 |
| 7N | 100 | 100 | 010 | 0 | Uab | -Uab | -IC | IC | 0 |
- 矩阵式整流器输入功率因数补偿算法(08-23)
- 矩阵式三相/单相电源研究(06-10)
- 大功率储能型有源箝位反激变换器的研究(02-28)
- 六种基本DC/DC变换器拓扑结构总结(12-12)
- 工程师自我养成之反激变换器控制环路仿真设计(12-09)
- 全桥变换器结构 软开关移相电源设计(12-07)
