EMI/EMC设计讲座（二）磁通量最小化的概念

　　在PCB中，会产生EMI的原因很多，例如：射频电流、共模准位、接地回路、阻抗不匹配、磁通量……等。为了掌握EMI，我们需要逐步理解这些原因和它们的影响。虽然，我们可以直接从电磁理论中，学到造成EMI现象的数学根据，但是，这是一条很辛苦、很漫长的道路。对一般工程师而言，简单而清楚的描述更是重要。本文将探讨，在PCB上「电的来源」、Maxwell方程式的应用、磁通量最小化的概念。

　　电的来源

　　与磁的来源相反，电的来源是以时变的电双极（electric dipole）来建立模型。这表示有两个分开的、极性相反的、时变的点电荷（point charges）互为相邻。双极的两端包含着电荷的变化。此电荷的变化，是因为电流在双极的全部长度内，不断地流动而造成的。利用振荡器输出讯号去驱动一个没有终端的（unterminated）天线，此种电路是可以用来代表电的来源。但是，此电路无法套用低频的电路原理来做解释。不考虑此电路中的讯号之有限传播速度（这是依据非磁性材料的介电常数而定），反正射频电流会在此电路产生。这是因为传播速度是有限的，不是无限的。此假设是：导线在所有点上，都包含相同的

　　电压，并且此电路在任何一点上，瞬间都是均衡的。这种电的来源所产生的电磁场，是四个变量的函数：

　　1. 回路中的电流振幅：电磁场和在双极中流动的电流量成正比。

　　2. 双极的极性和测量装置的关系：与磁来源一样，双极的极性必须和测量装置的天线之极性相同。

　　3. 双极的大小：电磁场和电流组件的长度成正比，不过，其走线长度必须只有波长的部份大。双极越大，在天线端所测量到的频率就越低。对特定的大小而言，此天线会在特定的频率下共振。

　　4. 距离：电场和磁场彼此相关。两者的强度和距离成正比。在远场（far field），其行为和回路源（磁的来源）类似，会出现一个电磁平面波。当靠近「点源（point source）」时，电场和磁场与距离的相依性增加。

　　近场（near field）（磁和电的成份）和远场的关系，如附图一所示。所有的波都是磁场和电场成份的组合。这种组合称作「Poynting向量」。实际上，是没有一个单独的电波或磁波存在的。我们之所以能够测量到平面波，是因为对一个小天线而言，在距离来源端数个波长的地方，其波前（wavefront）看起来像平面一样。

　　这种外貌是由天线所观测到的物理「轮廓」；这就好像从河边向河中打水漂一样，我们所看到的水波是一波波的涟漪。场传播是从场的点源，以光速的速度向外辐射出去；其中，。电场成份的测量单位是V/m，磁场成份的测量单位是A/m。电场（E）和磁场（H）的比率是自由空间（free space）的阻抗。这里必须强调的是，在平面波中，波阻抗Z0，或称作自由空间的特性阻抗，是和距离无关，也和点源的特性无关。对一个在自由空间中的平面波而言：

　　
波前所承载的能量单位是watts/m2。

　　就Maxwell方程式的大多数应用而言，噪声耦合方法可以代表等效组件的模型。例如：在两个导体之间的一个时变电场，可以代表一个电容。在相同的两导体之间，一个时变磁场可以代表互感（mutual inductance）。附图二表示这两种噪声耦合机制。

　　
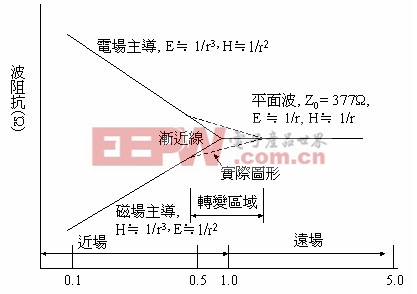
图一：波阻抗和距离的关系

　　平面波的形状

　　若要使此噪声耦合方法正确，电路的实际大小必须比讯号的波长小。若此模型不是真正正确时，仍然可以使用集总组件（lumped component）来说明EMC，原因如下：

　　1. Maxwell方程式不能直接应用在大多数的真实情况中，这是因为复杂的边界条件所造成的。如果我们对集总模型的近似正确度没有信心，则此模型是不正确的。不过，大多数的集总组件（或称作离散组件）是可靠的。

　　2. 数值模型不会显示噪声是如何根据系统参数产生的。纵使有一个模型可能是答案，但与系统相关的参数是不会被预知、辨识，和显现的。在所有可用的模型当中，集总组件所建立的模型算是最好的。

　　为什么这个理论和对Maxwell方程式的讨论，对PCB设计和布线（layout）很重要？答案很简单。我们必须先知道电磁场是如何产生的，之后我们就能够降低在PCB中，由射频产生的电磁场。这与降低电路中的射频电流有关。此射频电流直接和讯号分布网络、旁路和耦合相关。射频电流最后会形成频率的谐波和其它数字讯号。讯号分布网络必须尽量的小，如此才能将射频回传电流的回路区域尽量缩小。旁路和耦合与最大电流相关，而且必须透过电源分散网络来产生大电流；而电源分散网络，在定义上，它的射频回传电流之回路区域是很大的。

　　
图二：噪声耦合方法
　
　　Maxwell方程式的应用

到目前为止，Maxwell方程式的基本概念已经介绍过了。 但是，要如何将此物理和高等微