未知负载情况下PWM逆变器的自适应重复控制
1 引言
闭环调节的PWM逆变器已被广泛地应用于各种交流功率调节系统,例如UPS系统,自动电压调节器(AVR’S)和可编程交流源(PAS’S)。这些应用都要求系统在有暂态或周期性负载扰动时保持低失真波形。研究PWM逆变器闭环调节的目的是提高系统的动态响应,而以往的大多数研究工作都集中在了通过同步反馈控制来提高暂态响应 。虽然这些研究能够较好地克服暂态负载扰动,但当负载有周期性的扰动时,输出波形依然存在着周期性失真。
重复控制理论来源于内模原理 ,内模原理指出:系统在稳定状态下无稳态误差的跟踪参考输入信号的前提条件是闭环控制系统稳定且闭环控制系统中包含有参考输入信号的传递函数。它提供了一种消除由动态系统所产生的周期性误差的方法。重复控制器也可视为周期波产生器,它通过反馈控制器进行闭环调节,从而消除了周期性误差。为了降低对重复控制系统的苛刻要求,须对有限频率模式进行方案上的改进,对于时变系统可用自适应重复控制方案来消除周期误差 。本文所提出的这种新的自适应重复控制方案,采用辅助补偿器来稳定闭环系统,并通过一个自适应调谐控制器对其参数进行调谐。自适应重复控制器能在设备变化的条件下保证闭环的稳定性。
2 重复控制系统
2.1 重复控制原理
一台自动控制装置要求在有未知的或是不可测量的扰动输入时无稳态误差,并要求通过调节控制变量来跟踪相应的参考指令。在设计自动控制系统时,内模原理起到了至关重要的作用。内模原理提出 ,如果稳定的闭环系统中包括产生这些参考指令的模式,那么被控输出将在没有稳态误差的情况下跟踪一组参考输入。因此内模原理显示出其高精度,渐近性和跟踪特性,并且可以通过在控制环内对模型的定位来获取周期的外部输入信号。通过使用基于微处理器的数字控制器,可以很容易的实现重复控制方案。由于微处理器和DSP都具有很高的性能,所以控制环路中还包含了其他的频率模式,这充分表明了超精度自动控制系统方案的可行性。
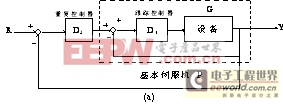
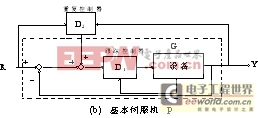
在重复控制系统中,除了传统的跟踪控制器外,还在控制环中插入了重复控制器。重复控制系统有多种控制结构,图1所示为重复控制系统的基本结构,其中(a)图为级联型重复控制器,(b)图提供了一条到重复控制器的前向反馈通道。跟踪控制器的主要目的是提高系统的暂态响应,从而使系统不受外界扰动的影响。
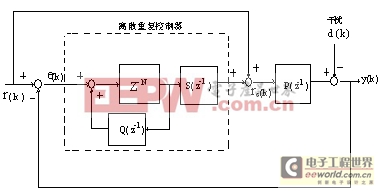
图2给出了离散时间重复控制系统的方框图,其中P(



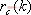
由图2可以看出,从干扰输入d(k)循迹误差e(k)的转移函数为:
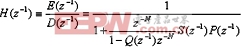
其中E(


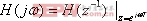
如果d(k)是以N为周期的干扰,那么d(k)的傅立叶级数可以表示为:
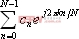
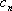


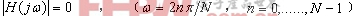
这表明这些周期误差的频率模式已经通过重复控制器被消除,在此情况下将获得良好的循迹效果。但同时也增加了合成S(



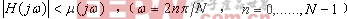
其中的
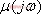
2.2 稳定性分析
从图2中我们可以得到:
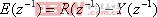
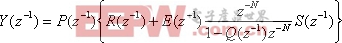
从(6)和(7)中消去Y(

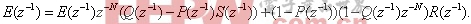
图3给出了(8)式的方框图,如果对任意
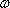
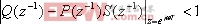
并且P(




相对稳定性和周期误差的收敛速度进行综合考虑。为简便起见,如果我们选择Q(







2.3 收敛性分析
在(9)式的稳定性标准中,也可以把
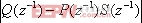
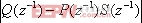
h =
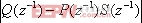
果h=0,那么在一个循环之后周期误差将被消除。然而,要满足这一条件需要有P(4)的完美匹配,但这显然是难以实现的。在此,我们定义:
S(
自适应重复控制 数字信号处理控制 脉宽调制逆变器 相关文章:
- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
