PWM开关变换器分析方法综述

一，将是数值仿真今后发展的一个重要方向[5]。

3 解析法又可分为离散法和连续法两大类。离散解析法采用差分方程和Ｚ变换技术。其优点是精确度

高，建模时基本不作任何假定，可用于任何开关变换器。但它只能求出控制输出波形函数，且分析程序复杂，所得结果更复杂，很难了解网络的性质，不能处理非理想开关，不能分析纹波。因此近年来离散法发展缓慢，而是朝着离散法与连续法结合的方向发展[10]。

连续解析法包括平均法（状态空间平均法、电路平均法）和渐进法。平均法采用微分方程和Ｓ变换的形式，并作一些数学处理，因此模型及结果都简单，但不如离散法精确，且输出纹波无法体现。其本质是平均，平均的目的是将时变电路变为非时变线性电路，在小信号的情况下可线性化，从而能用它来分析变换器的稳态以及小信号时的各种性质，从而线型电路的各种分析设计手段均可套用。

3.1 平均法

S. Cuk 和R.D Middle brook在1976年提出的状态空间平均法是目前使用最广泛、最具代表性的平均方法[11]。他们对状态变量进行了平均和线性化处理，给出描述开关变换器电路特性的一般解析式及其规范化化的等效电路形式。对于一个工作在连续导电模式下的PWM型DCDDDC变换器，其状态方程分别为

这就是著名的状态空间平均法。由上可知, 时变电路(1)(2)变成了非时变电路(3)，从而可求稳态工作点、小信号传递函数等。状态空间平均法是ＰＷＭ开关变换器的一个系统的分析方法，简明精确。但也存在着问题：稳定性分析不准确、不能分析纹波、无法分析准谐振变换器，且线性化方法只是局部处理，故不能用于大信号分析，对方程进行平均就意味着电路不出现高频成分，倘若高频成分起主要作用，则平均结果就不正确。在考虑了实际工作过程中输出反馈控制电路的工作特性对分析结果的影响后，F.C.Ｌee等提出了离散平均方法[12]，对状态进行平均处理而对输出结果进行采样离散化处理，得到了开关变换器电路的更加精确的描述方程和等效电路形式。为了便于计算机辅助分析，A. Pietkietwics 等基于开关变换器电路的拓扑性质提出一种利用节点方程和回路方程的平均方程[13]。但平均的条件是：开关变换器的输出低通滤波器的特征频率远小于开关频率，且电路的输出纹波较小。Brown等提出的抽样序列模型[14]保留了这个高频成分，因此模型更精确。从模型的推导来看，它对扰动不作平均正是保留了高频成分。其优点是提高了稳定性分析的精度，但它引入了冲击函数序列，处理麻烦，反馈网络的设计变得复杂。

连续平均法中的另外一种是平均值等效电路法。它是从原变换器出发进行电路处理，最后得出一个等效电路模型。在推导时，只是处理开关元件，而线性元件不变。如P. R. K. Chetty的电流注入等效分析法[15]，等效受控源法以及三端开关器件法[16]，它们都是从电路结构出发，利用时间平均技术而进行电路分析，但当电路元件增多，要得出平均后的拓扑结构需要很大的运算量。

围绕着拓扑不变这一要求，有不少处理方法诞生：Wester的电路平均法[17]；Y.S.Lee的MISSCO[18]和许建平的ECA法（Equivalent Circuit Approach），Voperian的简化开关模型（Ｖ模型）[19]以及Tymerski等用谐波平衡原理建立的开关模型（Ｔ模型）。

PWM开关模型对常见的开关变换器都适用。而Ｖ模型与Ｔ模型都是基于PＷＭ开关模型的概念。它们都是把开关从电路中独立出来，提出一个PWM开关模型DD单刀双掷开关。各端按所接元件性质的不同区分为三个端，分别接三极管、二极管和公共端。它对各类ＤＣDＤＣ变换器都适用。忽略电容的损耗电阻时,V模型与T模型推导的出发点相同。 对于PWM开关变换器, 都有下式:

若对(6)式进行小信号扰动分析即得Ｖ模型。更精确的，将扰动产生的响应分为基波和高次谐波，用谐波平衡原理，则得出Ｔ模型。因而，Ｖ模型是Ｔ模型的特例。两者的区别在于：前者是平均法，后者本质上是谐波平衡法；前者在时域中处理，后者在频域中处理；前者是一线性模型，且模型比较简单，适用于小信号分析，并可分析一些寄生效应；后者是一非线性模型，可用于大信号分析，并可用于波形失真的估计，它的一阶近似就是Ｖ模型。但Ｔ模型只可以考虑单频率的扰动，不能分析多频扰动，而且不能用于可能产生谐波的变换器的分析[20,26]。

3.2 渐近法

连续解析法的另一个分支是渐近法。其前提是待解方程存在小参量。 一般的，开关变换器的状态方程可写为：

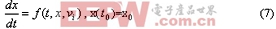
x是状态变量，v 为输入。对于理想开关，f有跳跃，但在Caratheoreodory意义下满足

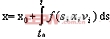
的x仍称为(４)的解[21]。因此，对（7）的求解有可能用