基于LCC谐振变换器的高压直流电源设计

摘要：为提高高压直流电源效率，降低其体积和重量，这里介绍了一种基于LCC谐振变换器的高压直流电源设计方法。结合移相脉宽调制(PWM)和脉冲频率调制(PFM)方法，实现变换器在全负载范围内的软开关。首先分析了LCC电路的工作原理，并采用基波近似法进行数学建模，在此基础上，给出不同负载时频率、占空比与电压增益的关系曲线，为设计LCC谐振变换器提供理论依据。最后通过一台峰值电压35 kV，额定功率7 kW的电源样机验证了设计的正确性，系统采用闭环控制，提高了输出电压的精度。

关键词：电源；高压直流；谐振变换器；软开关

1 引言

高频高压变压器是高压直流电源设计的难点，经过分析，如何减小变压器的分布参数是高频高压电源设计的关键。此处通过引入谐振，将变压器分布参数作为谐振元件的一部分，实现开关管的软开关，减小开关损耗，提高开关频率，从而减小变换器的体积。

谐振变换器有串联、并联和串并联3种拓扑。串并联谐振变换器，又称LCC谐振变换器，结合了前两种拓扑的优点，在合理设计参数的前提下，可使电源在输入电压范围变化很大，输出空载到满载的条件下，仍然保持很高的效率。LCC谐振变换器主要有移相PWM和PFM两种控制方法。这里采用PWM和PFM结合的控制策略，在频率变化范围不大，负载电压恒定的前提下，保证变换器从空载到满载范围内均能实现软开关。通过闭环控制，提高输出电压的抗干扰能力。

2 LCC谐振变换器工作原理

2．1 LCC谐振电路工作状态分析

图1为电容型滤波LCC谐振变换器电路。Cs，Ls为LCC谐振电路串联谐振电容和谐振电感，Ls包含变压器折算到初级的等效漏感；Cp为并联谐振电容，包含变压器折算到初级的分布电容。分析前先假设：输出电容很大，Uo保持不变；所有器件都是理想器件；电感电流连续且为理想正弦波。

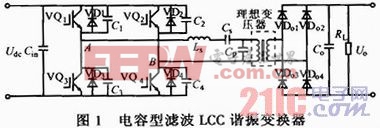
图2为移相PWM控制稳态时的主要波形。

(1)[t0～t1] t0时刻，电感电流iLs为零，此时VQ4为零电流开通，在前一时段VQ1已经零电压开通，VQ1，VQ4导通，uAB为正，Ls，Cs，Cp发生谐振，输出整流桥关断，uCp从-Uo／n升高，到t1时刻，uCp升高至Uo／n，输出整流桥导通，此阶段结束。

(2)[t1～t2] 谐振电流流经VQ1，VQ4，Ls，Cs发生谐振，uCp被箝位在Uo／n，电路由变压器传递能量。

(3)[t2～t3]t2时刻，VQ1关断，iLs给C1充电，C3放电，当C3电压为零时，VQ1～VQ3自然换向完成。由于C1的缓冲作用，VQ1关断时电压上升率很小，近似于零电压关断。

(4)[t3～t4] 在t3时刻，VQ1，VQ3导通，VQ3零电压开通，iLs为正，uAB为零，t4时刻，iLs即将减小至零时，VQ4零电流关断。

(5)[t4～t5] iLs流过VD2，VD3，uAB为负，t5时刻，iLs到零，半个周期结束。

t5开始，变换器开始另一半周期的工作，工作过程与上半周期对称，在此不再赘述。

通过以上分析可知，采用移相控制时，开关管不存在开通损耗。关断时，开关管电流转移到与其并联的缓冲电容上，电容限制了开关管两端的电压上升率，从而实现开关管零电压关断。每一个反并联二极管都是自然关断，不存在关断损耗。因此，相比硬PWM模式，采用LCC变换器时，开关损耗会大幅度减小，逆变器效率随之增大。

2．2 LCC谐振变换器稳态模型

为简化分析，使用各个变量的基波分量近似代替变量本身，然后用经典的线性交流分析法进行分析，设计出所需的谐振参数，这就是基波近似法的基本思想。将变压器初级电压和电流进行傅里叶变换后，取其基波分量，发现变压器初级电压基波分量的相位滞后于初级电流基波分量，变压器、整流桥、输出滤波器及负载组成的二端口网络呈容性。故可将变压器以后的模块等效为一个RC并联电路，如图3所示。图中，Re为等效电阻，Ce为等效电容。图中A，B两点电压的基波分量为：

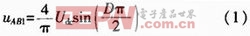
式中：Udc为逆变器的直流输入电压；D为PWM驱动信号的占空比。

在图3中，考虑D的影响，利用基波近似法，可得电压增益M为：

公式(2)中，k21为交流电压传输系数，其值为变压器初级电压的基波分量与A，B两点电压基波分量的比值，由图3可得其表达式为：

根据式(2)～(5)，绘制出不同负载下M与fsN的关系曲线(取α=1)，如图4a所示。通过调整电路参数，即可得合适的增益曲线和工作频率范围。图4a为选择不同增益谐振电路工作频率提供了依据。

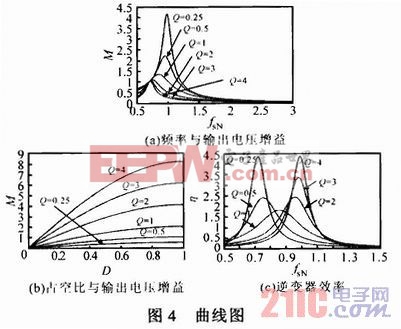
由图4a可知，从空载到满载变化时，fsN调节范围很大，而谐振元件确定后谐振频率就固定了，因此仅依靠变频控制需要开关频率变化范围很大。在调频基础上，配合调节D，能够在较小频率变化范围内，实现全负载范围内软开关，由式(2)～(6)得到不同负载下M与D的关系，图4b为移相调节时占空比的选择提供了理论依据。