工程师不可不知的开关电源关键设计（六）

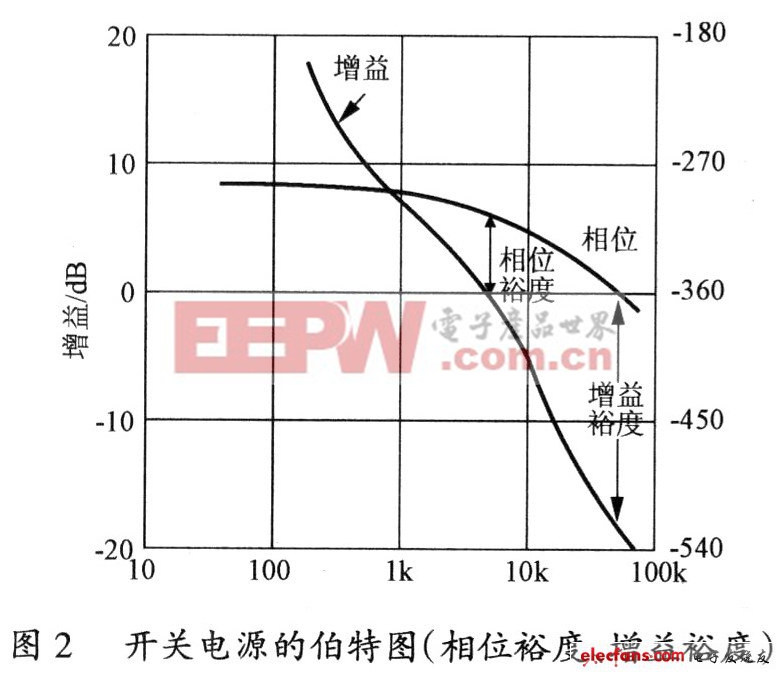
，主要包含输出电压采样、比较、放大（如TL431）、误差放大传输（如光电耦合器）和PWM集成电路内部集成的电压比较器（这些放大器的补偿设计最大程度的决定着开关电源系统稳定性，是设计的重点和难点）。

2 稳定性分析

如图1所示，假如在节点A处引入干扰波。此方波所包含的能量分配成无限列奇次谐波分量。如果检测到真实系统对不断增大的谐波有响应，则可以看出增益和相移也随着频率的增加而改变。如果在某一频率下增益等于l且总的额外相移为180°（此相移加上原先设定的180°相移，总相移量为360°），那么将会有足够的能量返回到系统的输入端，且相位与原相位相同，那么干扰将维持下去，系统在此频率下振荡。如图2所示，通常情况下，控制放大器都会采用反馈补偿元器件Z2减少更高频率下的增益，使得开关电源在所有频率下都保持稳定。

波特图对应于小信号（理论上的小信号是无限小的）扰动时系统的响应；但是如果扰动很大，系统的响应可能不是由反馈的线性部分决定的，而可能是由非线性部分决定的，如运放的压摆率、增益带宽或者电路中可能达到的最小、最大占空比等。当这些因素影响系统响应时，原来的系统就会表现为非线性，而且传递函数的方法就不能继续使用了。因此，虽然小信号稳定是必须满足的，但还不足以保证电源的稳定工作。因此，在设计电源环路补偿时，不但要考虑信号电源系统的响应特性，还要处理好电源系统的大信号响应特性。电源系统对大信号响应特性的优劣可以通过负载跃变响应特性和输入电压跃变响应特性来判断，负载跃变响应特性和输入电压跃变响应特性存在很强的连带关系，负载跃变响应特性好，则输入电压跃变响应特性一定好。

对开关电源环路稳定性判据的理论分析是很复杂的，这是因为传递函数随着负载条件的改变而改变。各种不同线绕功率元器件的有效电感值通常会随着负载电流而改变。此外，在考虑大信号瞬态的情况下，控制电路工作方式转变为非线性工作方式，此时仅用线性分析将无法得到完整的状态描述。下面详细介绍通过对负载跃变瞬态响应波形分析来判断开关电源环路稳定性。

3 稳定性测试

测试条件：

（1）无感电阻；

（2）负载变化幅度为10％~100％；

（3）负载开关频率可调（在获得同样理想响应波形的条件下，开关频率越高越好）；

（4）限定负载开关电流变化率为5A／μs或者2A/μs，没有声明负载电流大小和变化率的瞬态响应曲线图形无任何意义。

图3（a）为瞬变负载波形。

图3（b）为阻尼响应，控制环在瞬变边缘之后带有振荡。说明拥有这种响应电源的增益裕度和相位裕度都很小，且只能在某些特定条件下才能稳定。因此，要尽量避免这种类型的响应，补偿网络也应该调整在稍低的频率下滑离。

图3（c）为过阻尼响应，虽然比较稳定，但是瞬态恢复性能并非最好。滑离频率应该增大。

图3（d）为理想响应波形，接近最优情况，在绝大多数应用中，瞬态响应稳定且性能优良，增益裕度和相位裕度充足。

对于正向和负向尖峰，对称的波形是同样需要的，因此从它可以看出控制部分和电源部分在控制内有中心线，且在负载的增大和减少的情况下它们的摆动速率是相同的。

上面介绍了开关电源控制环路的两个稳定性判据，就是通过波特图判定小信号下开关电源控制环路的相位裕度和通过负载跃变瞬态响应波形判定大信号下开关电源控制环路的稳定性。下面介绍四种控制环路稳定性的设计方法。

4 稳定性设计方法

4．1 分析法

根据闭环系统的理论、数学及电路模型进行分析（计算机仿真）。实际上进行总体分析时，要求所有的参数要精确地等于规定值是不大可能的，尤其是电感值，在整个电流变化范围内，电感值不可能保持常数。同样，能改变系统线性工作的较大瞬态响应也是很难预料到的。

4．2 试探法

首先测量好脉宽调整器和功率变换器部分的传递特性，然后用“差分技术”来确定补偿控制放大器所必须具有的特性。

要想使实际的放大器完全满足最优特性是不大可能的，主要的目标是实现尽可能地接近。具体步骤如下：

（1）找到开环曲线中极点过零处所对应的频率，在补偿网络中相应的频率周围处引入零点，那么在直到等于穿越频率的范围内相移小于315°（相位裕度至少为45°）；

（2）找到开环曲线中EsR零点对应的频率，在补偿网络中相应的频率周围处引入极点（否则这些零点将使增益特性变平，且不能按照期望下降）；

（3）如果低频增益太低，无法得到期望的直流校正那么可以引入一对零极点以提高低频下的增益。

大多数情况下，需要进行“微调”，最好的办法是采用瞬态负载测量法。