基于电流测试的混合电路故障诊断

随着电子技术的飞速发展和制造工艺的不断提高，使得电路的复杂程度不断增加，芯片尺寸日益减小，使得系统级芯片上集成了越来越多的混合信号电路，而不再是单单的数字电路或者模拟电路。由于数模两种电路的测试方法不同，传统的测试已经不能满足发展的需求，这给仪器设备的设计者、使用者、维护者带来了前所未有的挑战，也使得数／模混合信号电路的检测日益受到业内人士的高度重视。本文提出的基于电流测试的混合电路故障诊断正是在这样的背景下提出的。

1 电流测试的理论知识

电流测试就是指通过测量电源电流并从中有效提取电路的故障信息，最终实现对电路故障的检测与定位。包括静态电流测试技术IDDQ和动态电流测试技术IDDT。

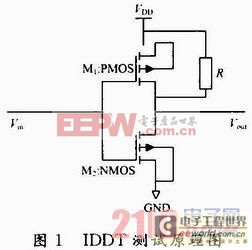
电路正常工作时，静态电流非常小，但是存在缺陷的电路静态电流非常大，所以当检测到电路中的静态电流出现异常，即可判定电路出现了故障。这也正是IDDQ测试的原理。但是，CMOS电路中某些故障，如开路故障等，并不引起静态电流的异常。因此，有必要在此引进动态电流测试。本文也正是基于此考虑了静态电流和动态电流测试的结合，而并非单纯的静态电流测试。IDDT是一个短暂导通的电流，即CMOS电路状态转换过程中，PMOS晶体管和NMOS晶体管同时导通，使得在电源与地之间形成了一个导通电路，如图1所示。由于IDDT是电路在动态转换过程中电流的变化情况，因此IDDQ的大小并不影响它的结果。所以，这也避免了深亚微米电路不断增长的静态漏电流对测试的影响。本文正是研究两者的结合在混合电路故障诊断中的重要意义。

2 小波神经网络对混合电路故障诊断
小波神经网络(Wavelet Neural Network)是小波分析理论与人工神经网络ANN理论相结合。目前，二者的结合有如下两种途径：
(1)松散型结合。即小波分析作为神经网络的前置处理手段，为神经网络提供输入特征向量。
(2)紧致型结合。小波和神经网络直接融合，即小波函数和尺度函数形成神经元。
本文采用松散型的小波与神经网络的结合。先通过PSPICE进行正常电路与故障电路建模仿真，提取静态电流IDDQ和动态电流IDDT参数，并在Matlab中运用小波分析对所得到的电流进行特征提取，并结合神经网络进行具体分析。步骤如下：
(1)参数的提取。在PSPICE中提取正常电路及具有桥接故障、开路故障等多种故障电路的电流信息。
(2)小波分析。对(1)中得到的电流信息在Matlab中进行小波分解，提取小波系数，并进一步计算RMS。
(3)故障定位。将小波分析与BP神经网络结合，分析判断其定位效果，具体步骤如图2所示。

3 混合电路故障诊断实例
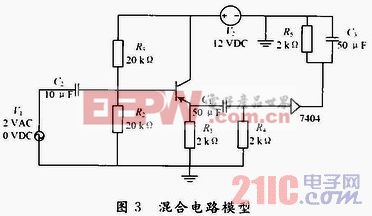
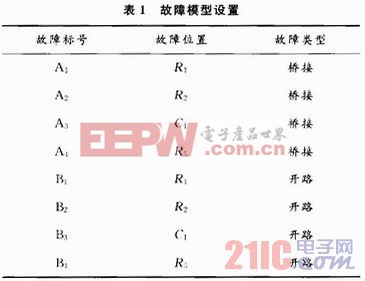
在PSPICE中用以7404与共集电极放大电路组成的混合电路进行故障模型的研究，其电路模型如图3所示。通过灵敏度分析可知R1，R2，R5，C1对于电路的影响较大。在电路中设置4个桥接故障、4个开路故障，如表1所示。虽然生产过程中导致电路缺陷各式各样，但根据各种缺陷的失效机理，可以采用各种各样的故障模型来等效。本文对于桥接故障，采用在桥接点之间连接一个电阻建立故障模型，阻值分别取10 Ω，1 kΩ和1 MΩ来对应相对小、近似相等、相对大。而对于开路故障，采用在开路点接入10 MΩ点电阻来建立故障模型。

3．1 IDDQ在混合电路故障检测中的应用
在PSPICE中对各个故障模型进行仿真，可以很容易得出静态电流值。IDDQ对于混合电路的桥接故障可以很明显地看出漏电流的区别，但是它却检测不出开路故障。
3．2 IDDT在混合电路故障检测中的应用
对于在PSPICE中得到的正常电路及开路故障动态电流信息，在Matlab中进行5层小波变换，得出小波系数。再通过均方根误差来体现它们之间的差别。均方根误差用式(1)来定义：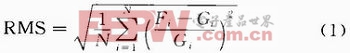

式中：Fi为开路故障的小波系数；Gi为正常电路的小波系数；N为小波系数的个数。通过式(1)得出RMS的值，见表2。

所以，通过前面两节的分析可以看出，静态电流测试和动态电流测试的结合可以明显地提高混合电路的故障覆盖率，为今后进行混合电路故障诊断起到了一定的指导意义。
3．3 小波特征提取与BP神经网络的结合
(1)能量特征的提取。电路的电流信息进行5层小波分解，得到高频小波分解系数及低频小波分解系数向量(d5，…，d1，a5)。其中，高频系数的提取在Matlab中用detcoef函数，而低频系数提取足采用appcoef函数。再把各系数向量组合成能量特征向量：
F=(Ed5…Ed1，Ea5)
(2)确定BP神经网络结构和参数。BP神经网络输入神经元个数由测试节点决定；隐层个数可通过“试凑法”和式(2)粗略地估计。

式中：m，n和l分别为隐层节点数、输入节点数、输出节点数；a为1～10之间不确定的数。
经过反复试验，本文的BP神经网络结果为6-7-4。
(3)训练BP神经网络。电路仿真时进行20次Monte Carlo分析产生20个样本，其中10个为训练样本．另外10个测试样本。本文总共要进行4组训练。网络训练误差曲线如图4所示。从图中可以知道，网络经过4432步训练达到了目标误差。