一种用于SVPWM技术中的死区补偿方法

摘要：提出一种用于空间矢量脉宽调制(SVPWM)的死区补偿方法。该方法根据电流极性及6个非零电压空间矢量间的位置关系，确定了所需补偿的电压空间矢量，仅需在每个PWM周期内对部分PWM脉宽进行修正就能有效改善由死区效应引起的输出波形畸变，减小误补偿随时间积累所产生的影响，减少CPU运行时间。最后通过TMS320LF2407A型DSP实现该补偿算法，并在110 kW感应电机变频调速系统中验证了其有效性。
关键词：逆变器；死区补偿；空间矢量脉宽调制

1 引言
设计逆变器时，为防止上下桥臂出现直通，通常需设置一个死区时间以延迟开关器件的导通。但死区时间的存在使实际输出的电压、电流波形发生畸变，电机转矩发生脉动，且在低速或轻载时这种影响尤其严重。因此对死区的补偿问题已成为变频调速系统中必须解决的关键问题。
现有文献的死区补偿方法可分为硬件补偿和软件补偿两类。其中硬件补偿需要额外的硬件电路，使系统结构复杂化，成本增加，实际中较少采用；软件补偿通过在控制程序中加入补偿算法来实现死区补偿，它无需添加硬件，且更加灵活，具有广泛的适用性。软件补偿大体上又可分为两种：①通过计算需要补偿的电压平均值来进行补偿。该方法易于实现，但补偿精度低，较少用；②目前应用较多的是基于脉冲的死区补偿方法，即直接在本周期内对逆变器的6个PWM脉宽同时进行修正，从而补偿因死区时间而损失或增加的输出电压。该方法理论上可对死区时间进行较准确的补偿。但实际系统中补偿的准确程度取决于电流极性检测的正确与否。一旦电流极性检测错误，必然导致误补偿，不但不能消除死区对系统的影响，反而会使此影响加重。
这里在分析死区的产生及其影响的基础上，针对SVPWM方式提出了一种新型的基于脉冲的死区补偿方法，该方法仅需在每个PWM周期里对部分PWM脉宽进行修正。在一台110 kW感应电机进行实验，结果验证了该方法的有效性。

2 死区效应分析
图1示出典型的电压源型逆变电路，以该电路为例分析死区效应的影响，负载为异步电动机。为便于分析，不考虑开关器件导通和关断时间，且逆变电路采用SVPWM控制。以A相为例，在死区时间内逆变器上、下桥臂的功率开关器件均关断，且由于电磁惯性使得电动机绕组中的电流不会立即反向，而是通过续流二极管续流。则当iA>0时，电流通过VD4续流，A桥臂对直流的中点电位uAO'=-Ud／2；iA0时，iA通过VD1续流，uAO'=Ud／2。

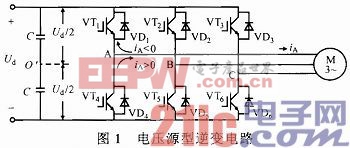
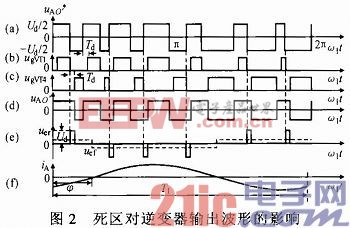
图2a为不考虑死区影响情况下uAO'的理想波形。考虑死区时间Td影响后，A相桥臂功率开关器件VT1与VT4的实际驱动信号分别见图2b，c。图2d为考虑Td影响后实际的uAO'波形。图2e为由于死区影响产生的电压偏差脉冲uer，且uer=uAO'*-uAO'，其正、负与电流极性有关。图2f为iA波形。

3 死区补偿方法
由图2e，f知，iA>0时，uAO'比MAO'*多出一系列负序脉冲，相当于下桥臂多作用了Td；iA0时，uAO'比uAO'*多出一系列正序脉冲，相当于上桥臂多作用了Td。死区补偿就是根据当前相电流的极性对下一个PWM脉宽进行修正。
SVPWM方法通过调整每个扇区两个相邻非零电压空间矢量和零矢量作用时间的长短合成所需的电压空间矢量，以保证该矢量的轨迹为圆形。为易于阐述本方法，令图1中上桥臂导通为1，下桥臂导通为0。电压扇区的划分如图3所示。6个非零电压空间矢量将逆变器的一个工作周期等分为6个区域。以iA>0，iB0，iC0时为例，在Td里，相当于A相桥臂的下桥臂多导通了Td，B相桥臂的上桥臂多导通了Td，C相桥臂的上桥臂多导通了Td，即由于死区的影响会使在该PWM周期内多出一个作用了Td时间的空间矢量(0 1 1)，因此，要增加Td时间的空间矢量(1 0 0)来抵消这个多余的空间矢量。

具体补偿方法与电压空间矢量所在的扇区、电流极性及需补偿的空间矢量有关。下面根据图3，给出iA>0，iB0，iC0时，电压空间矢量位于6个不同扇区内的补偿方法。分两种情况讨论：①在一个PWM周期里，与该电压扇区相邻的两个非零电压矢量中包含该需补偿的电压空间矢量，则直接在该电压空间矢量的期望脉宽基础上增加Td；②与该电压扇区相邻的两个非零空间矢量不包含这个需补偿的电压空间矢量，则可通过这两个非零电压空间矢量与其余4个非零电压空间矢量之间的位置关系推导出这个需补偿的电压空间矢量，从而在不改变每个电压扇区内作用的原有电压空间矢量前提下对相应的PWM脉宽进行修正。以下分别对这两种情况进行具体说明：①当iA>0，iB0，iC0时，需补偿的电压空间矢量为(1 0 0)，此时若电压空间矢量位于I扇区，与该扇区相邻两个非零电压空间矢量为(1 0 0)和(1 1 0